
Òàêèì îáðàçîì, äëÿ äàííîé ñèñòåìû äèôôåðåíöè-
àëüíûå óðàâíåíèÿ ñâîáîäíûõ êîëåáàíèé èìåþò âèä
×àñòíîå ðåøåíèå ýòèõ óðàâíåíèé:
q
=
A
sin(
kt
+
β
);
r
=
B
sin(
kt
+
β
),
ãäå
À
è
Â
— àìïëèòóäû ãëàâíûõ êîëåáàíèé;
k
— ÷àñ-
òîòû ñâîáîäíûõ êîëåáàíèé;
β
— íà÷àëüíàÿ ôàçà êî-
ëåáàíèé.
Óðàâíåíèå ÷àñòîò, âûòåêàþùåå èç äàííîé ñèñòå-
ìû äèôôåðåíöèàëüíûõ óðàâíåíèé, èìååò âèä
(
ñ
11
–
à
11
k
2
)(
ñ
22
–
à
22
k
2
)–
ñ
12
2
= 0.
Êîðíè ýòîãî áèêâàäðàòíîãî óðàâíåíèÿ, ñîîòâåò-
ñòâóþùèå êâàäðàòàì ÷àñòîò, îïðåäåëèì ïî ôîðìóëå
Ïóñòü â ðàññìàòðèâàåìîé çàäà÷å ìàññû îäíî-
ðîäíûõ äèñêîâ
m
1
= 0,18 êã,
m
2
= 0,18 êã, êîýôôè-
öèåíòû æåñòêîñòè ïðóæèí
ñ
1
=
ñ
2
=
ñ
3
= 135 Í/ì,
òîãäà
a
11
= (3/2)
m
1
= 0,27 êã;
ñ
11
=
c
1
+
ñ
3
= 270 Í/ì;
c
12
=
ñ
3
= 135 Í/ì;
a
22
= (3/2)
m
2
= 0,36 êã;
c
22
=
c
2
+
+
c
3
= 270 Í/ì. Ñëåäîâàòåëüíî, ÷àñòîòû ñâîáîäíûõ
êîëåáàíèé
k
1
= 500 ñ
-1
;
k
2
= 1500 ñ
-1
.
Êîýôôèöèåíòû ðàñïðåäåëåíèÿ, ñîîòâåòñòâóþ-
ùèå ÷àñòîòàì
k
1
è
k
2
, â îáùåì ñëó÷àå èìåþò âèä
 äàííîì ñëó÷àå
μ
1
= –0,43;
μ
2
= 3,46. Óðàâíåíèÿ,
îïðåäåëÿþùèå ïåðâîå ãëàâíîå êîëåáàíèå, ïðèìóò
ñëåäóþùèé âèä:
q
1
=
A
1
sin(500
t
+
β
1
);
r
1
= –0,43
A
1
sin(500
t
+
β
1
).
Óðàâíåíèÿ, îïðåäåëÿþùèå âòîðîå ãëàâíîå êîëåáàíèå:
q
2
=
A
2
sin(1500
t
+
β
2
);
r
2
= 3,464
A
2
sin(1500
t
+
β
2
).
Îáùåå ðåøåíèå äèôôåðåíöèàëüíûõ óðàâíåíèé
ïðåäñòàâëÿåò ñîáîé ñóììó ÷àñòíûõ ðåøåíèé:
q
=
q
1
+
q
2
=
A
1
sin(500
t
+
β
1
)+
A
2
sin(500
t
+
β
2
);
r
=
r
1
+
r
2
= 0,43
A
1
sin(1500+
β
1
)+3,46
A
2
(1500
t
+
β
2
).
Çíà÷åíèÿ
À
i
è
β
i
îïðåäåëÿþòñÿ ïî íà÷àëüíûì óñ-
ëîâèÿì çàäà÷è.
Ïîëó÷åííûå ðåøåíèÿ ïîçâîëÿþò óñîâåðøåíñòâî-
âàòü êîíñòðóêöèþ ðàáî÷åé êàìåðû, ðàçìåùàÿ àáðà-
çèâíûå ýëåìåíòû â òåõ çîíàõ öèëèíäðè÷åñêîé îáå-
÷àéêè, ãäå êëóáåíü, êîíòàêòèðóþùèé ñî ñòåíêîé êà-
ìåðû, íàèáîëåå èíòåíñèâíî ïðèæèìàåòñÿ ê ðàáî÷åé
ïîâåðõíîñòè. Ýòè çîíû îïðåäåëÿþòñÿ ñ ó÷åòîì ñêî-
ðîñòè âðàùåíèÿ êëóáíÿ êàðòîôåëÿ è ñîáñòâåííîé
÷àñòîòû êîëåáàíèé ðàññìîòðåííîé ñèñòåìû èç òðåõ
ïðèëåæàùèõ ê ðàáî÷åé ïîâåðõíîñòè êëóáíåé.
 îáùåì ñëó÷àå íà ãåîìåòðèþ ðàñïîëîæåíèÿ àá-
ðàçèâíûõ ïîëîñ äîëæíû âëèÿòü óïðóãèå õàðàêòå-
ðèñòèêè ïðóæèí — ìîäóëè óïðóãîñòè ìÿêîòè êàð-
òîôåëÿ. Ñëåäîâàòåëüíî, ó÷åò ñåçîííûõ èçìåíåíèé
ñòðóêòóðíî-ìåõàíè÷åñêèõ ñâîéñòâ êàðòîôåëÿ òðåáó-
åò ïðèìåíåíèÿ ðàçëè÷íûõ ðàáî÷èõ îðãàíîâ ïðè î÷è-
ñòêå ñâåæåñîáðàííîãî êàðòîôåëÿ è êàðòîôåëÿ, ïðî-
øåäøåãî îïðåäåëåííûé ñðîê õðàíåíèÿ. Êðîìå òîãî,
íà ÷àñòîòó êîëåáàíèé è ñîîòâåòñòâåííî íà òðåáóå-
ìóþ øèðèíó àáðàçèâíûõ ïîëîñ áóäåò âëèÿòü ìàññà
î÷èùàåìûõ êëóáíåé.
Ïðèìåíèâ ñèñòåìó Mathcad, îöåíèì ÷èñëåííî
ïîëó÷åííûå ðåçóëüòàòû äëÿ ñëåäóþùåãî èíòåðâàëà
èçìåíåíèé ìàññû êëóáíåé è êîýôôèöèåíòà æåñò-
êîñòè êàðòîôåëÿ. Ìàññó ïðèìåì èçìåíÿþùåéñÿ îò
m
1
= 0,18 êã äî
m
1
= 0,27 êã, à êîýôôèöèåíò æåñò-
êîñòè — îò
c
1
= 135 Í/ì äî
c
1
= 160 Í/ì (ïðè÷åì ïðè
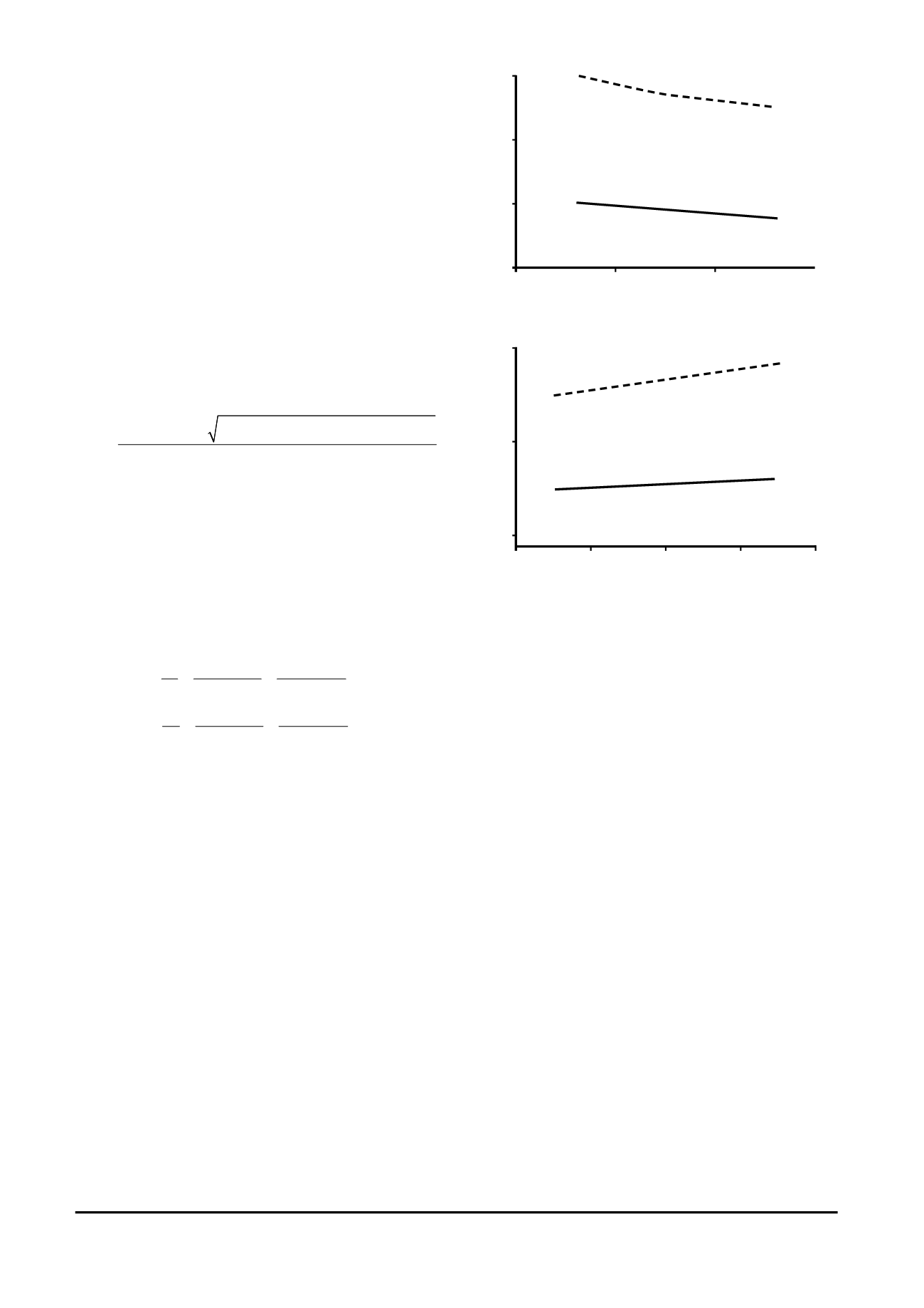
õðàíåíèè æåñòêîñòü óìåíüøàåòñÿ). Ïîñòðîèì ãðà-
ôèêè çàâèñèìîñòè ÷àñòîò
k
1
è
k
2
îò ìàññû êëóáíÿ
è åãî æåñòêîñòè (ðèñ. 2).
Îäíà èç âîçìîæíîñòåé óëó÷øåíèÿ êà÷åñòâà î÷è-
ñòêè êàðòîôåëÿ â êàìåðàõ êîíóñíûõ êàðòîôåëå-
î÷èñòèòåëüíûõ ìàøèí — çàìåíà áîêîâûõ âñòàâîê
53
ХРАНЕНИЕ И ПЕРЕРАБОТКА СЕЛЬХОЗСЫРЬЯ, № 2, 2012
11
11
12
22
12
22
0;
0 .
a q c q c r
a c r c r
+ + =
+ + =
(
)
(
)
2
2
11 22
22 11
11 22
22 11
11 22 11 22
12
2
1,2
11 22
4
.
2
a c a c
a c a c
a a c c c
k
a a
+
+
−
−
=
∓
2
2
1
11
11 1
12
12 1
1
2
2
1
12
12 1
22
22 1
2
2
2
11
11 2
12
12 1
2
2
2
2
12
12 2
22
22 2
`
`
;
`
`
`
`
.
`
`
B n a k n a k
A n a k n a k
B n a k n a k
A n a k n a k
−
−
μ = =
=
−
−
−
−
μ = =
=
−
−
à
1
2
1500
1000
500
0
0,15
0,2
0,25
m
1
(
i
)
2000
1000
0
130
140
150
160
170
с
1
(
i
)
á
Ðèñ. 2. Çàâèñèìîñòü ÷àñòîò k
1
è k
2
îò ìàññû êëóáíÿ (à) è åãî
æåñòêîñòè (á): 1 – k
2
(
i
)
; 2 – – k
2
(
i
)
2
1
Электронная Научная СельскоХозяйственная Библиотека









