
Научный журнал НИУ ИТМО. Серия «Процессы и аппараты пищевых производств» № 3, 2016
26
Объекты и методы исследований
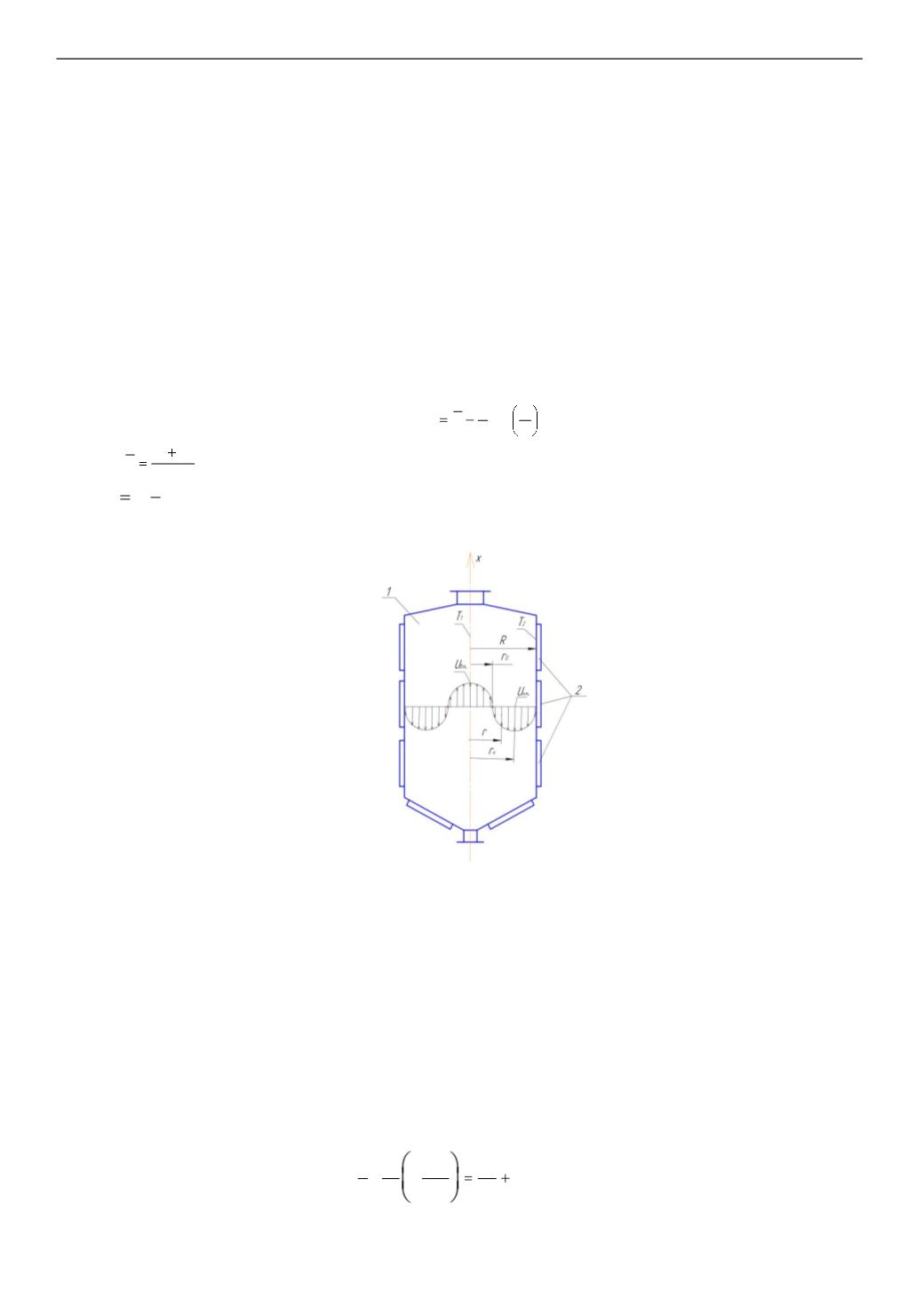
Объектом теоретического исследования будет служить цилиндроконический бродильный аппарат,
в котором температура жидкости около стенки ниже, чем в центре. Источник тепловой энергии
сосредоточим в нижней части аппарата. Им может быть, например, трубчатый электронагреватель,
обеспечивающий стационарный нагрев жидкости. В этом случае жидкость, находящаяся около стенки
будет двигаться вниз, а в центре аппарата – вверх (рисунок 1). Регулирование скорости движения
жидкости по высоте можно осуществлять либо изменением температуры хладоносителя, либо
изменением подачи его в теплообменные секции.
Гидродинамика
В решении задачи по поиску уравнения, описывающего профиль локальных скоростей по радиусу
аппарата, мы будем следовать работе [1, с. 305], приняв режим движения жидкости в аппарате
ламинарным и распределение температуры по сечению аппарата линейным, т.е.
1
Δ
2
r
T T T
R
,
(1)
где
Т
и
1 2
2
T T
T
– текущие и средние значения температур, °C соответственно;
1
2
Δ
T T T
,
1
T
и
2
T
– температуры в центре и на стенке аппарата, °C соответственно;
r
– текущий радиус, м;
R
– радиус аппарата, м.
Рисунок 1 – Схема цилиндроконического бродильного аппарата:
1 – бродильный аппарат; 2 – теплообменные секции
Сразу же отметим, что принятие условий ламинарного течения и линейности профиля температуры
по живому сечению аппарата на данном этапе вызвано лишь стремлением упростить решение задачи.
Следует иметь в виду, что температура в центре аппарата будет определяться мощностью теплового
источника, находящегося внутри потоков жидкости. Этим источником являются дрожжевые клетки.
В этой связи температурный профиль в аппарате следует искать из уравнения Фурье-Кирхгофа [1, 3] для
варианта с движением жидкости при наличии внутреннего источника энергии.
Однако для этого необходимо иметь уравнение, описывающее профиль локальных скоростей по сечению
аппарата. Для его вывода воспользуемся уравнением Навье-Стокса. В случае установившегося
осесимметричного движения гомогенной жидкости вдоль оси
x
под действием массовой силы, силы
трения и сил давления оно в цилиндрических координатах будет иметь вид:
1 d d
d
μ
ρ
d d
d
x
u
p
r
g
r r
r
x
,
(2)
Электронная Научная СельскоХозяйственная Библиотека









