
Научный журнал НИУ ИТМО. Серия «Процессы и аппараты пищевых производств» № 3, 2016
28
Так как расход жидкости через любое сечение определяется известным уравнением
d
x
s
Q u S
,
то после подстановки в него уравнения (8) или (9), значения
dS
и соответствующих пределов
интегрирования запишем:
0
0 3
3
0
0
0
в
в
2π
d 2π (
) d
9
r
r
x
A
Q
u r r
r r r r
,
(11)
3
3
0
0
3
н
2π
d 2π
(
)
ln d
9
R
R
xн
m
r
r
A
R
Q
u r r
r R r
r r
r
.
(12)
Значения средних скоростей каждого из потоков находим из уравнения неразрывности потока: для
нисходящего потока –
/
н
н н
w Q S
, для восходящего потока
–
в
в в
/
w Q S
,
где
н
S
и
в
S
– площади сечений
нисходящего и восходящих потоков.
Результаты и их обсуждение
Рассмотрим конкретный пример движения жидкости в условиях свободной конвекции в аппарате
радиусом
1, 5
R
м, при разности температур
Δ 0, 25 C
T
. Жидкость обладает следующими физическими
свойствами:
3
β 0,1 10
град
-1
,
ρ 1000
кг/м
3
,
3
μ 1, 3 10
Па·с.
Для определения радиуса
0
r
воспользуемся программой MathCad и подпрограммой:
0
0, 0001
r
Given
0
0
н
в
0
Q r Q r
0
0
r MinErr r
0
0,927
r
.
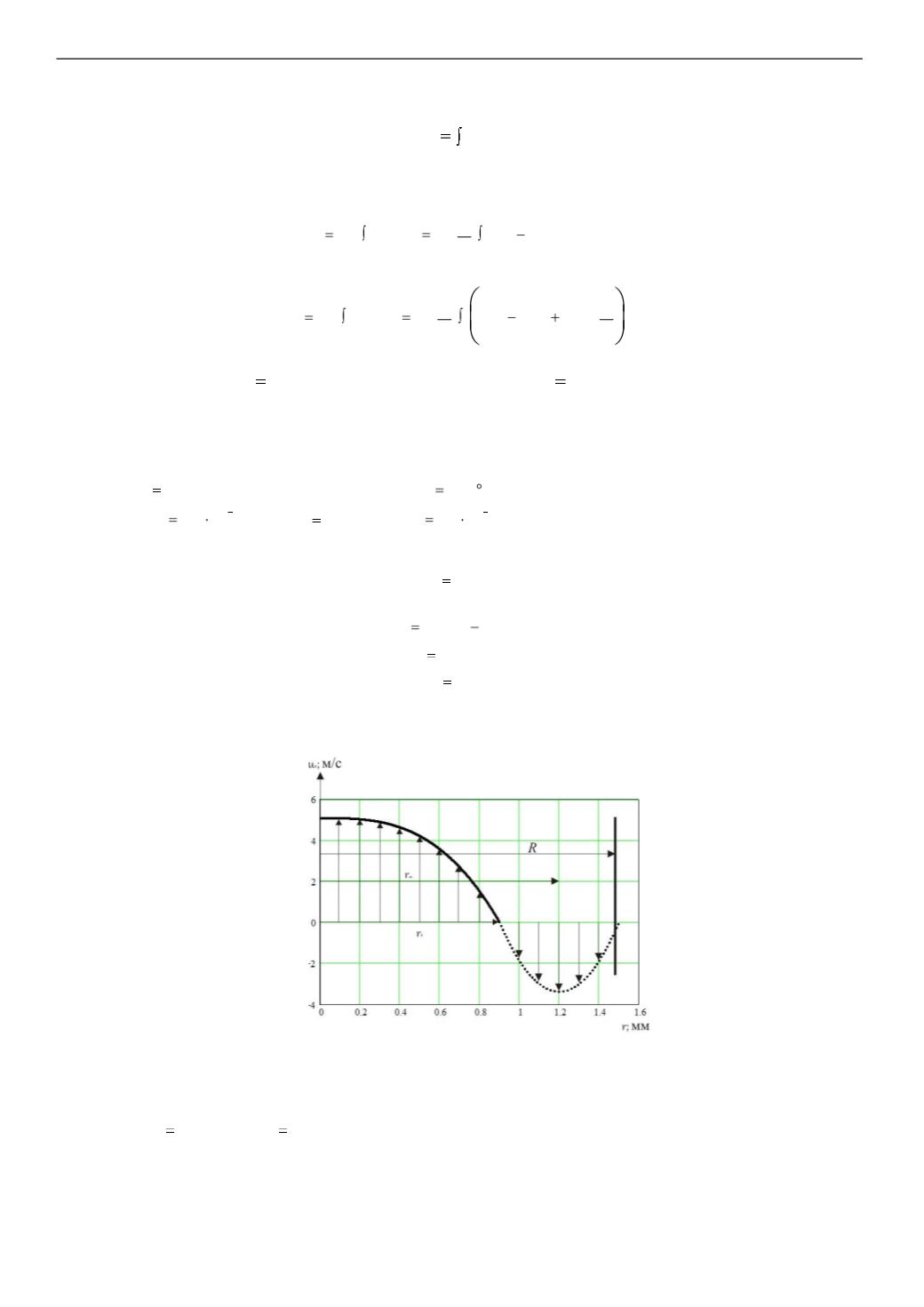
Результаты расчетов, представленные на рисунке 2 в виде графического изображения профиля
скорости по радиусу аппарата, позволяют сделать определенные выводы.
Рисунок 2 – Изменение локальных скоростей по радиусу аппарата
Линии соответствуют: — уравнению (8); ·· уравнению (9)
Во-первых, средние значения скоростей движения жидкости в восходящем и нисходящем потоках
различны (
в
w 3, 33
м/с,
н
w 2, 076
м/с) и они настолько высоки, что течение не может быть ламинарным.
Ламинарный режим возможен при очень малых значениях
Δ .
T
Во-вторых, при турбулентном режиме движения жидкости профиль скорости по сечению потока
отличается от профиля при ламинарном течении. Турбулентные потоки, согласно двухслойной модели
Прандтля, делятся на две зоны, в которых профили скоростей описываются системой двух уравнений [1, 3]
Электронная Научная СельскоХозяйственная Библиотека









