
В
иноделие
и
иноградарство
5/2011
27
виноделие
в странах зарубежьЯ
описывающее вариации парциального
давления O
2
в надвинном пространстве
бутылки, имеет вид
Если предположить, что скорость
связывания O
2
в вине значительно пре-
вышает скорость его диффузии через
поверхность вина и пробку, можно счи-
тать, что
C
O
ви
2
но
≈
0
(конкретно это означа-
ет, что у кислорода не было времени ак-
кумулироваться в матрице
вино
). В этом
случае можно переписать предыдущее
уравнение следующим образом:
Maтематически парциальное давление
O
2
в надвинном пространстве укупорен-
ной бутылки подчиняется так называемо-
му
дифференциальному уравнению перво-
го порядка со вторым постоянным членом
(предполагая, что объем воздушной каме-
ры головки, диффузные длины и коэффи-
циент диффузии кислорода через проб-
ку не изменяются с течением времени)
[8–12]. Гипотеза не бесспорна, так как из-
вестно, что механические свойства проб-
ки изменяются с годами, а вино может по-
степенно испаряться (увеличивая, таким
образом, объем надвинного простран-
ства). Тем не менее, данное уравнение
допускает следующее аналитическое ре-
шение:
t
P
O
П
2
Г
(
t
)
≈
(
P
O
П
2
Г
(0) –
a
τ
) exp –— +
a
τ
, (9)
τ
где
P
O
П
2
Г
(0)
— начальное парциальное дав-
ление O
2
в надвинном пространстве голов-
ки (сразу же после укупорки бутылки):
и
В теории, принимая во внимание урав-
нение (9), парциальное давление O
2
в бу-
тылке стремится к асимптотическому зна
чению, обозначенному
P
O
П
2
Г
(
∞
)
, и после
выдержки в течение некоторого време-
ни 5
τ
(предположим, спустя всего лишь
несколько дней) составит для воздушной
камеры объемом порядка 5 мл:
Это предельно допустимое значение
зависит от физико‑химических харак-
теристик вина и проницаемости укупо-
рочного материала (см. коэффициент
диффузии по отношению к O
2
,
D
O
пр
2
обка
).
Для натуральной пробки, проницаемость
которой к кислороду составляет порядка
нескольких мкл в день, парциальное дав-
ление O
2
в надвинном пространстве будет
составлять несколько десятков паскалей,
всего лишь менее одной тысячной значе-
ния атмосферного давления. После уку-
поривания бутылки парциальное давле-
ние кислорода будет постепенно падать,
стремясь к этому предельно допустимому
значению (рис. 3).
Уравнение (9) моделирует изменения
парциального давления O
2
в воздушной
камере бутылки. Однако с точки зрения
вина этот параметр не является столь су-
щественным. Что действительно важно —
это общая масса кислорода, с которым
оно будет контактировать на протяжении
своей жизни.
Проникновение кислорода в вино с те-
чением времени — диффузионный про-
цесс, описываемый следующим урав-
нением (которое является не чем иным,
как членом, называемым
кислородо
сборник
, дифференциального уравнения,
определяющего число молей O
2
в воздуш-
ной камере головки):
Итак, мы ранее определили изменение
парциального давления O
2
в надвинном
пространстве бутылки с течением време-
ни. Таким образом, подставляя вместо ве-
личины
P
O
П
2
Г
ее теоретическое выражение,
рассчитанное выше, получим:
Интегрируя данное дифференциальное
уравнение и умножая на молярную массу
кислорода, получаем теоретическое из-
менение его массы, обозначенное
m
O
2
,
с которой вино будет находиться в кон-
такте по истечении некоторого времени
выдержки
t
:
Для временных интервалов свыше не-
скольких десятков дней (
t
>> τ
) уравнение
упростится и примет вид
Обозначения:
P
O
at
2
m
— парциальное давление O
2
в ат-
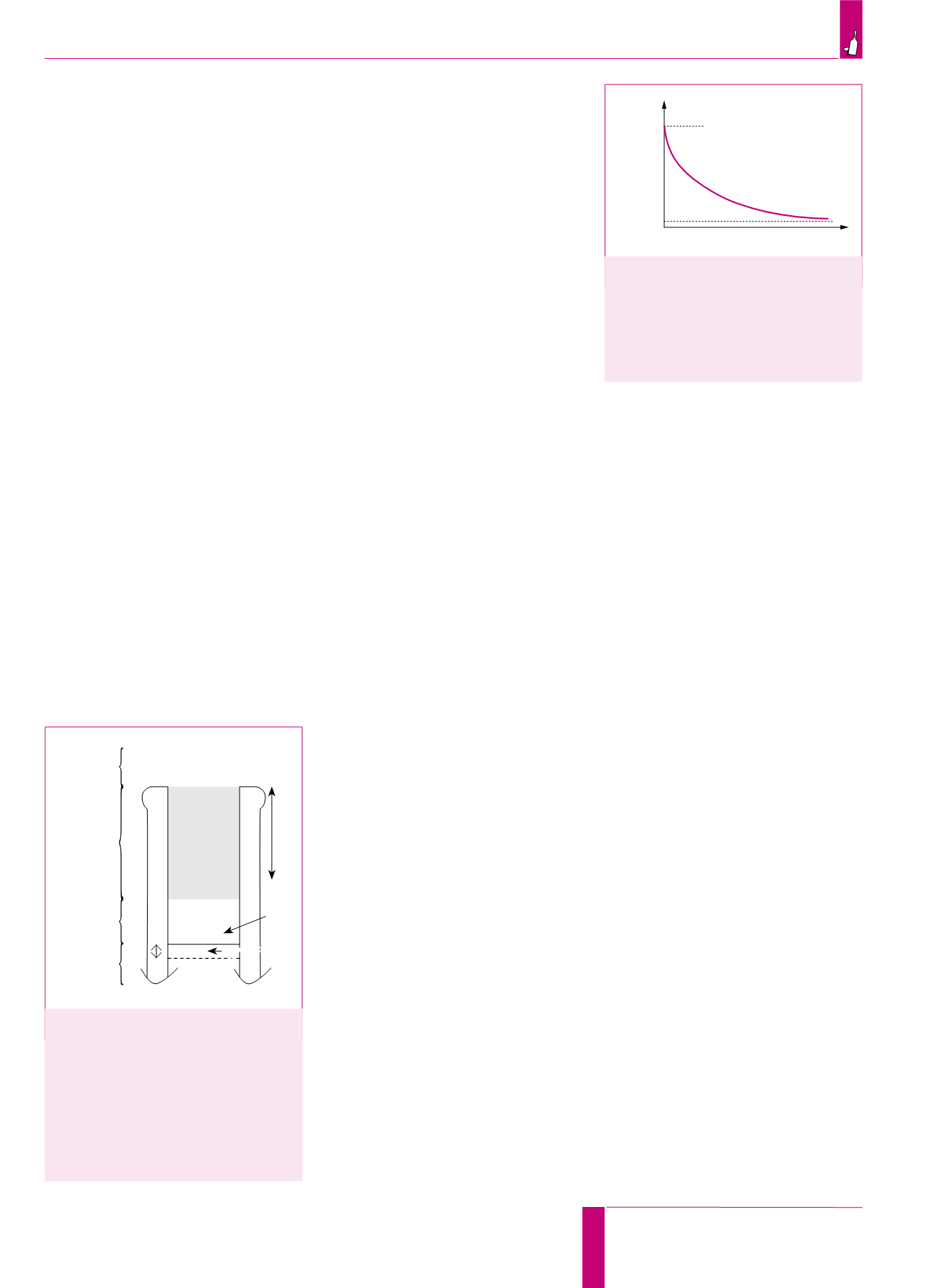
Рис. 3.
Теоретическое экспоненциальное
уменьшение парциального давления
O
2
в надвинном пространстве после
укупорки бутылки [начиная со значения
сразу же после укупорки
Р
ПГ
О
2
(0)
до значения равновесия
Р
ПГ
О
2
(
∞
)],
связанное с постепенным растворением
кислорода в вине
P
O
2
ПГ
(0)
P
O
2
ПГ
P
O
2
ПГ
(
∞
)
t
Рис. 2.
Схематическое изображение горлышка
укупоренной бутылки и совокупности
параметров модели, представленное
в синтетической форме показателей
концентраций и парциального давления
свободного и растворенного кислорода
в трех компартаментах (атмосфера,
надвинное пространство бутылки
и вино). Данная принципиальная схема
для кислорода действительна для любого
другого присутствующего газа
C
O
2
вино
V
ПГ
C
O
2
равн
=
P
O
2
вино
P
O
2
ПГ
C
O
2
atm
,
P
O
2
atm
λ
пробка
C
O
2
ПГ
,
P
O
2
ПГ
λ
вино
Атмосфера
Пробка
Надвинное
пространство
Вино
λ
вино
D
O
пр
2
обка
P
O
at
2
m
P
O
П
2
Г
(
∞
) =
a
τ ≈
————
—————————
λ
пробка
D
O
ви
2
но
RTH
O
ви
2
но
dn
O
П
2
Г
(
C
O
at
2
m
–
C
O
П
2
Г
)
——— =
D
O
пр
2
обка
S
——————— –
dt
λ
пробка
(
C
O
ра
2
вн
–
C
O
ви
2
но
)
–
D
O
ви
2
но
S
————————
.
λ
вино
(7)
dP
O
П
2
Г
S
(
P
O
at
2
m
–
P
O
П
2
Г
)
——— =
D
O
пр
2
обка
——
——————— –
dt V
ET
λ
пробка
S
(
H
O
ви
2
но
P
O
П
2
Г
–
C
O
ви
2
но
)
–
D
O
ви
2
но
——
——————————
.
V
ПГ
λ
вино
(8)
S
D
O
пр
2
обка
P
O
at
2
m
a
=
——
——————
V
ПГ
λ
пробка
V
ПГ
V
ПГ
λ
вино
τ
=
——————————————
≈
————————
.
D
O
пр
2
обка
D
O
ви
2
но
SD
O
ви
2
но
RTH
O
ви
2
но
S
|
————+———RTH
O
ви
2
но
|
λ
пробка
λ
вино
dn
O
2
(
C
O
Ге
2
нри
–
C
O
ви
2
но
)
—— =
D
O
ви
2
но
S
————————
≈
dt
λ
вино
C
O
Ге
2
нри
H
O
ви
2
но
P
O
П
2
Г
≈
D
O
ви
2
но
S
——— =
D
O
ви
2
но
S
—————
.
λ
вино
λ
вино
(11)
dn
O
2
H
O
ви
2
но
t
—— =
D
O
ви
2
но
S
———
(
P
O
П
2
Г
(0)
– a
τ
)exp
–
—
+
a
τ
.
dt
λ
вино
τ
(12)
V
ПГ
P
O
П
2
Г
(0)
D
O
пр
2
обка
P
O
at
2
m
m
O
2
(
t
)
≈
M
O
2
————— +
M
O
2
S
——————
t
.
RT
λ
пробка
RT
H
O
ви
2
но
τ
m
O
2
(
t
) =
M
O
2
D
O
ви
2
но
S
————
×
λ
вино
t
×
(
P
O
П
2
Г
(0)
– a
τ
)
1 – exp
–—
a
τ
.
τ
(13)
(14)
(10)
Электронная Научная СельскоХ зяйственная Библиотека









