ЭлБиб

основание прямоугольника высоты v/ (nh), где h - длина интервала,

v - число выборочных значений случайной величины, попавших в

этот интервал. Площадь каждого прямоугольника v/nh • h= v/n

представляет собой частоту соответствующей группы реализаций

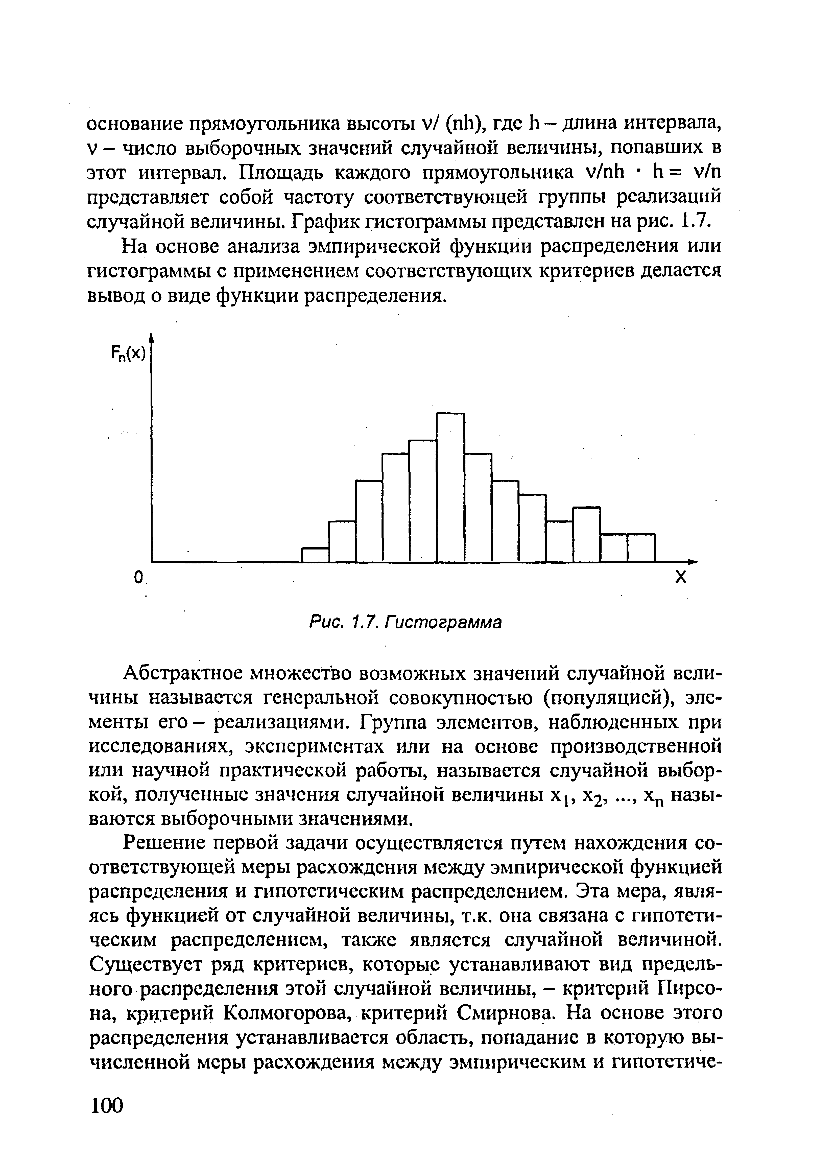
случайной величины. График гистограммы представлен на рис. 1.7.

На основе анализа эмпирической функции распределения или

гистограммы с применением соответствующих критериев делается

вывод о виде функции распределения.

Рис. 1.7. Гист ограмма

Абстрактное множество возможных значений случайной вели

чины называется генеральной совокупностью (популяцией), эле

менты его - реализациями. Группа элементов, наблюденных при

исследованиях, экспериментах или на основе производственной

или научной практической работы, называется случайной выбор

кой, полученные значения случайной величины Xj, х2, ..., хп назы

ваются выборочными значениями.

Решение первой задачи осуществляется путем нахождения со

ответствующей меры расхождения между эмпирической функцией

распределения и гипотетическим распределением. Эта мера, явля

ясь функцией от случайной величины, т.к. она связана с гипотети

ческим распределением, также является случайной величиной.

Существует ряд критериев, которые устанавливают вид предель

ного распределения этой случайной величины, - критерий Пирсо

на, критерий Колмогорова, критерий Смирнова. На основе этого

распределения устанавливается область, попадание в которую вы

численной меры расхождения между эмпирическим и гипотстиче-

100

Научная Эле тронная СельскоХозяйственная Библиотека