
КОНДИТЕРСКОЕ ПРОИЗВОДСТВО
•
4/2012
29
ТЕХНОЛОГИИ ПРОИЗВОДСТВА
ния функции отклика в двух параллельных
опытах.
Установили, что в соответствии с критери-
ем Фишера уравнение регрессии первого
порядка, полученное по результатам ПФЭ,
не адекватно описывает эксперименталь-
ные данные. В связи с чем приняли решение
перейти к планированию второго порядка.
Второй этап
заключался в построении
математической модели в виде уравнения
регрессии второго порядка, отражающего
зависимость плотности сбивной массы (
y
)
от дозировок белка (
x
1
) и пектина (
x
2
).
Для этого в исходную матрицу планиро-
вания включили опыты в «звездных» точках
(табл.2,опыты5–8).Выборвеличины«звездно-
го» плеча
±
1,41 обусловлен необходимостью
получения униформ-ротатабельного плана,
обеспечивающего получение одинаковой
величины дисперсии предсказания для лю-
бой точки в пределах изучаемой области.
Опыты в «звездных» точках реализовали
в двухкратной повторности.
Статистическая обработка экспери-
ментальных данных заключалась в вычисле-
нии оценок регрессионных коэффициентов,
проверке их значимости, оценке воспроиз-
водимости опытов и установлении адекват-
ности полученного регрессионного уравне-
ния. При этом использовали статистические
критерии Стьюдента, Кохрена и Фишера
(при доверительной вероятности 95%).
Уравнение регрессии, адекватно опи-
сывающее зависимость плотности сбивной
массы (
y
) от изучаемых факторов, имеет
вид уравнения второго порядка:
, (1)
где
Х
i
– кодированные значения факто-
ров, связанные с натуральными значения-
ми
X
i
соотношениями:
Х
1
= (
x
1
– 6,25)/1,25;
Х
2
= (
x
2
– 2,50)/1,25. (2)
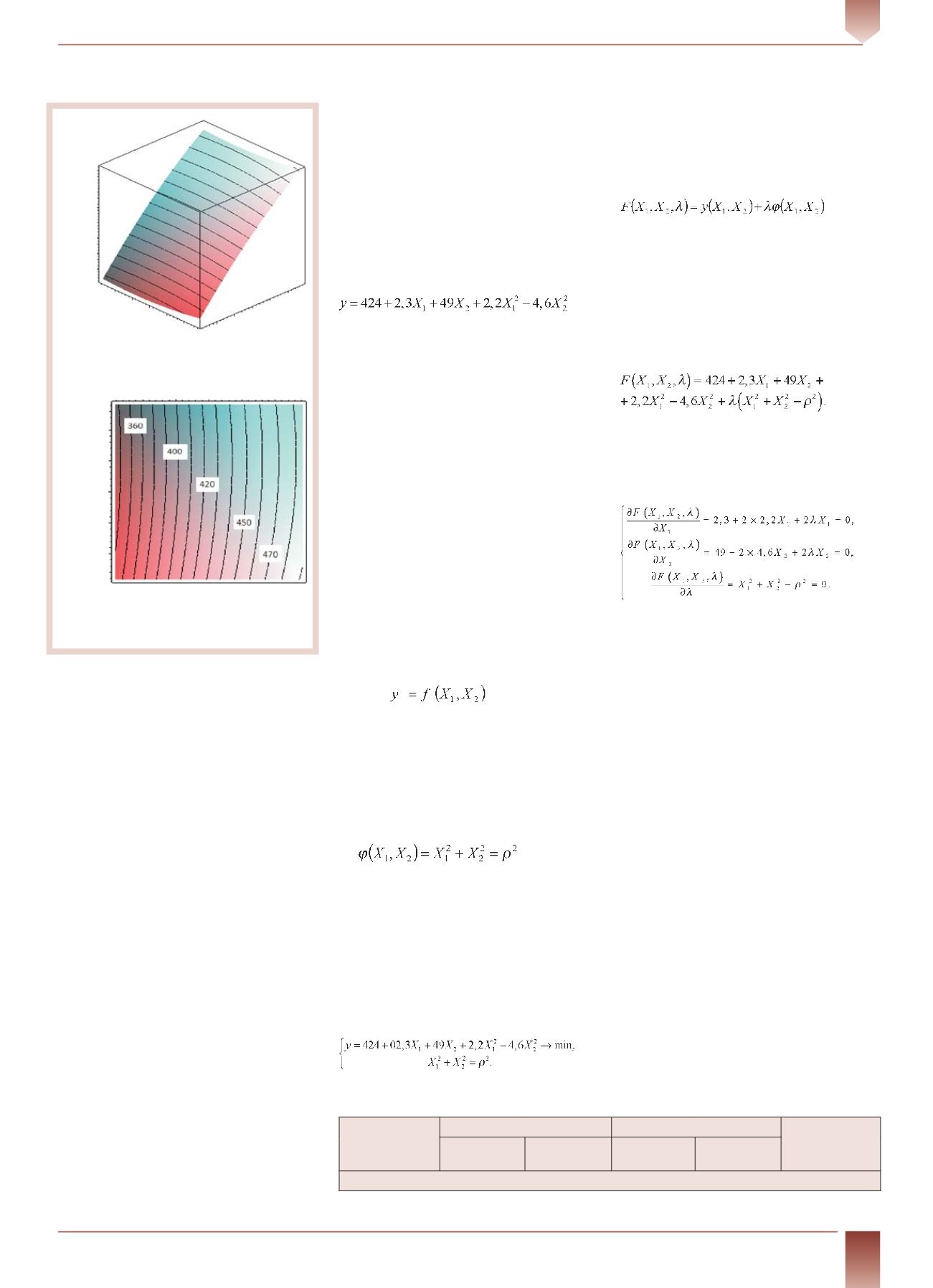
Графическая интерпретация зависи-
мости (1) в виде поверхности отклика и
линий равного уровня представлена на
рисунке.
Третий этап
заключался в оптимизации
структурно-механических свойств сбивной
массы.
Для поиска оптимальных параметров
Х
1
и
Х
2
задачу оптимизации сформулировали
так: необходимо найти значения независи-
мых переменных
Х
1
и
Х
2
, обеспечивающих
условный экстремум (минимум) функции
отклика
. Величины незави-
симых переменных
Х
1
и
Х
2
при этом не долж-
ны выходить за область эксперимента, гра-
ницы которой определяются значениями
факторов в «звездных» точках. Указанное
ограничение аналитически может быть за-
писано в виде выражения:
, (3)
которое в факторном пространстве
(для случая двух независимых переменных)
представляет собой сферу радиусом
ρ
(центр ее расположен в точке факторного
пространства
Х
1
= 0 и
Х
2
= 0).
Такимобразом, постановка задачи опти-
мизации аналитически записывается как
(4)
Поставленную задачу оптимизации (4)
решали, используя метод неопределенных
множителей Лагранжа. Для этого состави-
ли целевую функцию вида
, (5)
где
λ
– неопределенный множитель Ла-
гранжа.
С учетом уравнения регрессии (1)
и ограничения (3), которое накладывается
на независимые переменные, целевую
функцию (5) представили как
(6)
Дифференцируя уравнение (6) по пере-
менным,
Х
1
и
Х
2
λ
, составили систему урав-
нений
. (7)
Для решения системы уравнений (7)
при фиксированном значении радиуса
сферы
ρ
с последующим вычислением зна-
чения функции отклика по уравнению ре-
грессии (1) воспользовались интегрирован-
ным математическим пакетом MAPLEW 8.
Графическийанализ двумерных сечений
поверхности отклика (см. рисунок) пока-
зал, что минимальное значение параметра
оптимизации (
y
) достигается на границе
области эксперимента, чему соответствует
ρ
= 1,41. В связи с этим поиск оптимальных зна-
чений независимых переменных проводили
при указанном значении радиуса сферы.
Решая систему уравнений (7), получи-
ли оптимальные кодированные значения
переменных,
Х
1
и
Х
2
, при которых плотность
сбивной массы имеет минимальное значе-
ние, т. е. достигается условный экстремум
функции отклика (табл. 3).
Переходя от кодированных значений
к натуральным переменным, по формулам
(2) нашли оптимальные значения дозиро-
вок белка и пектина (см. табл. 3).
Таблица 3
Радиус сферы,
ρ
Кодированные значения
Натуральные значения
Плотность
сбивной массы,
кг/м
3
Дозировка
белка,
Х
1
Дозировка
пектина,
Х
2
Дозировка
белка,
Х
1
, г
Дозировка
пектина,
Х
2
, г
1,41
–0,048
–1,41
6,25
0,74
345
Плотность, кг/м
3
Дозировка белка, г
480
460
440
420
400
380
360
–1
–1
–1
–1
–0,5
–0,5
–0,5
–0,5
Х
1
Х
1
Х
2
Х
2
0
0
0
0
0,5
0,5
0,5
0,5
1
1
1
1
Дозировка пектина, г
Линии равного уровня плотности
сбивной массы (числа на кривых –
значения плотности, кг/м
3
)
Электронная Научная С льскоХозяйственная Библиотека









