
Ñðåäíÿÿ ñêîðîñòü øêèâà îïðåäåëåíà ïî ôîðìóëå
Ω
=
ϕ
+
ω
/2
π
,
(4)
ãäå
ϕ
+
— ïåðåìåùåíèå øêèâà îòíîñèòåëüíî ëåíòû
â ïîëîæèòåëüíîì íàïðàâëåíèè.
Îòìåòèì â îáùèõ ÷åðòàõ ïîñëåäîâàòåëüíîñòü
ðåøåíèÿ çàäà÷è. Ïåðâûé èíòåãðàë óðàâíåíèÿ (1) â
ïðåäåëàõ îò
δ
l+
äî òåêóùåãî çíà÷åíèÿ ôàçîâîãî
óãëà
δ
ïðåäñòàâëÿåò ñîáîé çàâèñèìîñòü ñêîðîñòè
ϕ.
(
δ
) øêèâà îòíîñèòåëüíî ëåíòû ïðè
Z
+
=
Z
++
. Åñëè
Z
++
≤
0,217, òî ñêîëüæåíèå øêèâà îòíîñèòåëüíî ëåí-
òû ïðîèñõîäèò ïðè íåèçìåííîì çíà÷åíèè áåçðàç-
ìåðíîãî ïàðàìåòðà ñîïðîòèâëåíèÿ
Z
+
=
Z
++
îòíîñè-
òåëüíîìó ñêîëüæåíèþ. Ïîýòîìó ïîñëå îïðåäåëåíèÿ
ôàçîâîãî óãëà
δ
2+
îêîí÷àíèÿ ñêîëüæåíèÿ øêèâà îò-
íîñèòåëüíî ëåíòû ïðè óñëîâèè
ϕ.
(
δ
) = 0 îïðåäåëÿþò
ϕ
+
, âû÷èñëÿÿ èíòåãðàë ôóíêöèè
ϕ.
(
δ
) â ïðåäåëàõ îò
ϕ
= 0 äî
ϕ
=
ϕ
+
è îò
δ
=
δ
+
äî
δ
2+
.
Åñëè æå
Z
++
> 0,217, òî äâèæåíèå øêèâà îòíîñè-
òåëüíî ëåíòû íà÷èíàåòñÿ ïðè
Z
+
=
Z
++
. Çàòåì ïîñëå
èçìåíåíèÿ íàïðàâëåíèÿ àáñîëþòíîé ñêîðîñòè øêè-
âà íà ïðîòèâîïîëîæíîå, ïðè ôàçîâîì óãëå
δ
=
δ
*
+
,
îíî ïðîäîëæàåòñÿ ïðè
Z
+
=
Z
++
äî ïðåêðàùåíèÿ
ñêîëüæåíèÿ øêèâà îòíîñèòåëüíî ëåíòû ïðè ôàçî-
âîì óãëå
δ
+
=
δ
2+
. Ôàçîâûé óãîë
δ
*
+
îïðåäåëÿþò èç
óñëîâèÿ ðàâåíñòâà íóëþ àáñîëþòíîé ñêîðîñòè
ϕ.
2
øêèâà. Òàêèì îáðàçîì, â ýòîì ñëó÷àå äâèæåíèå
øêèâà îòíîñèòåëüíî ëåíòû èìååò äâà èíòåðâàëà:
ïåðâûé
δ
l+
≤ δ ≤ δ
*
+
, ïðè ýòîì
Z
+
=
Z
++
è
ϕ.
2
> 0; âòî-
ðîé
δ
*
+
≤ δ ≤ δ
2+
, ïðè ýòîì
Z
+
=
Z
+-
è
ϕ.
2
< 0. Ïîëíîå
ïåðåìåùåíèå øêèâà îòíîñèòåëüíî ëåíòû
ϕ
+
=
ϕ
+1
+
ϕ
+2
,
(5)
ãäå
ϕ
+1
— ïåðåìåùåíèå øêèâà îòíîñèòåëüíî ëåíòû
íà ïåðâîì èíòåðâàëå, ðàâíîå èíòåãðàëó îò ôóíêöèè
ϕ.
(
δ
) â ïðåäåëàõ îò
ϕ
= 0 äî
ϕ
=
ϕ
+
è îò
δ
=
δ
1+
äî
δ
*
+
;
ϕ
+2
— ïåðåìåùåíèå øêèâà îòíîñèòåëüíî ëåíòû íà
âòîðîì èíòåðâàëå, ðàâíî èíòåãðàëó îò ôóíêöèè
ϕ.
(
δ
)
â ïðåäåëàõ îò
ϕ
= 0 äî
ϕ
=
ϕ
+2
è îò
δ
=
δ
*
+
äî
δ
2+
.
Çàìåòèì, ÷òî ìàêñèìóì óñêîðåíèÿ øêèâà îïðå-
äåëÿåòñÿ ñëåäóþùèì îáðàçîì: åñëè
Z
++
> 0,217, òî
îí ðàâåí àìïëèòóäíîìó çíà÷åíèþ óñêîðåíèÿ ëåí-
òû, ò.å.
ϕ
0
ω
2
, åñëè
Z
++
≤
0,217, òî
ϕ
0
ω
2
sin
δ
2
.
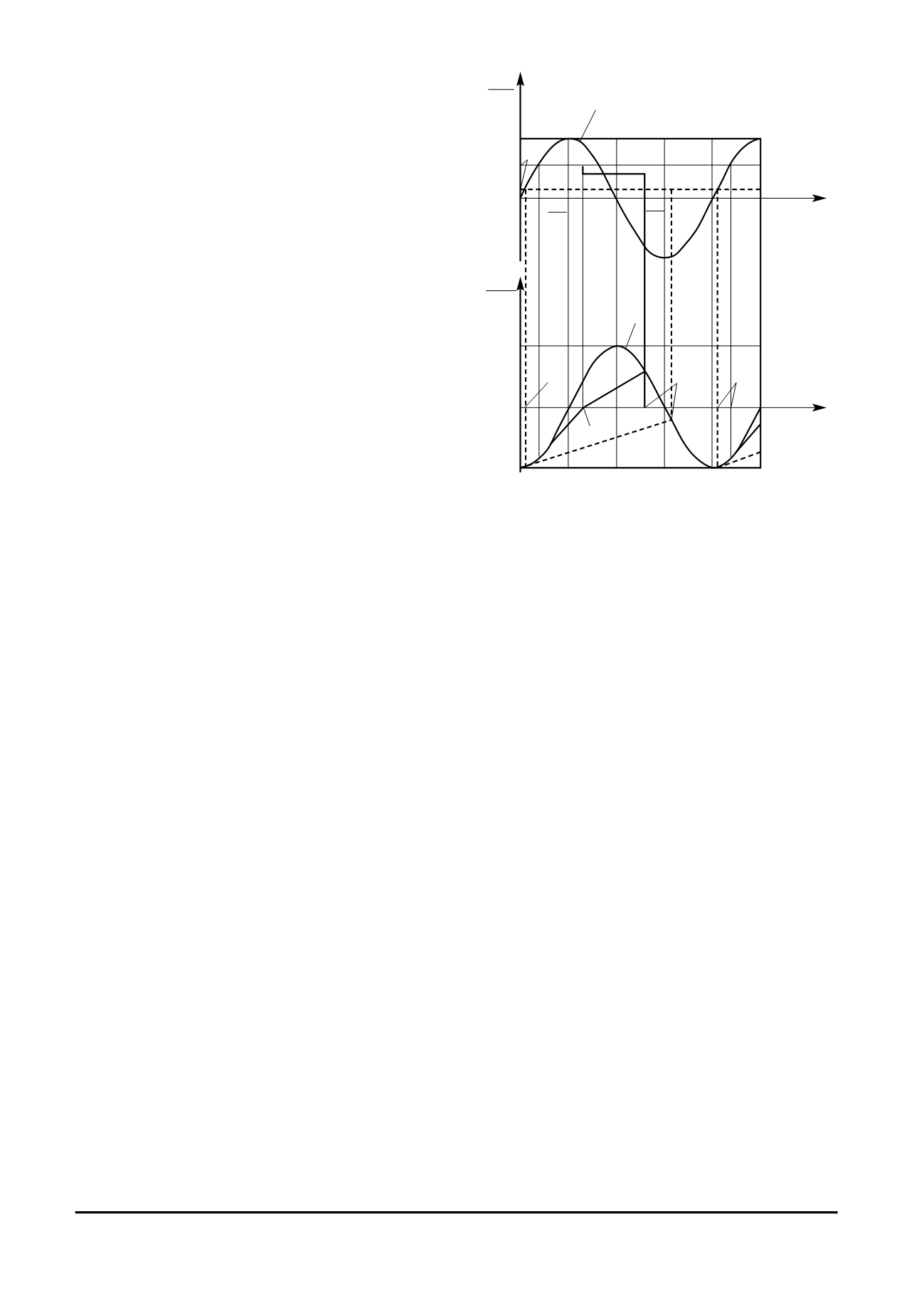
Íà ðèñ. 2 ïðåäñòàâëåíà ãðàôè÷åñêàÿ èíòåðïðåòà-
öèÿ ðåøåíèÿ äèôôåðåíöèàëüíîãî óðàâíåíèÿ äâè-
æåíèÿ øêèâà îòíîñèòåëüíî ëåíòû (èç ðàáîò Â.Â.Ãîð-
òèíñêîãî è åãî ó÷åíèêîâ [1]). Ïîñòðîåíèÿ ïóíêòè-
ðîì ñîîòâåòñòâóþò ñëó÷àþ
Z
++
< 0,217. Êàê âèäíî èç
ðèñóíêà, çà ïåðèîä êîëåáàíèé ëåíòû øêèâ èìååò
ñëåäóþùèå èíòåðâàëû äâèæåíèÿ: 0
≤ δ ≤ δ
l+
— äâè-
æåíèå øêèâà ñîâìåñòíî ñ ëåíòîé (áåç îòíîñèòåëü-
íîãî ïðîñêàëüçûâàíèÿ);
δ
l+
≤ δ ≤ δ
2+
— ñêîëüæåíèå
øêèâà îòíîñèòåëüíî ëåíòû;
δ
2+
<
δ
< 2
π
– äâèæåíèå
øêèâà ñîâìåñòíî ñ ëåíòîé.  ñëó÷àå
Z
+
+
> 0,217 èí-
òåðâàë ñêîëüæåíèÿ øêèâà îòíîñèòåëüíî ëåíòû ðàç-
áèâàþò íà äâà ïîäûíòåðâàëà:
δ
l+
≤ δ ≤ δ
*
+
— ñêîëü-
æåíèå ïðè
Z
+
=
Z
++
è ïðè
ϕ.
2
> 0;
δ
*
+
≤ δ ≤ δ
2+
ïðè
Z
+
=
Z
-
+
è
ϕ.
2
< 0.
Ñëåäóåò çàìåòèòü, ÷òî äàííûé ïðèâîä îáåñïå÷è-
âàåò âàðüèðîâàíèå ñðåäíåé óãëîâîé ñêîðîñòè âûõîä-
íîãî çâåíà (øêèâà) â äîñòàòî÷íî øèðîêîì äèàïàçî-
íå çíà÷åíèé, îäíàêî ñ óâåëè÷åíèåì óãëîâîé ñêîðî-
ñòè øêèâà óìåíüøàåòñÿ åãî óãëîâîå óñêîðåíèå.
Ïðèâîä áûë èñïûòàí â ñêàëüïåðàòîðå ñ ïîäà÷åé
èñõîäíîé çåðíîñìåñè íà íàðóæíóþ ïîâåðõíîñòü
ðåøåòíîãî öèëèíäðà, æåñòêî ñâÿçàííîãî ñ âûõîä-
íûì çâåíîì ïðèâîäà [2]. Ïðèìåíåíèå ïðèâîäà ïî-
çâîëèëî äîáèòüñÿ ïîâûøåíèÿ òåõíîëîãè÷åñêîé ýô-
ôåêòèâíîñòè î÷èñòêè ïøåíèöû îò ãðóáûõ è êðóï-
íûõ ïðèìåñåé ïî ñðàâíåíèþ ñî ñêàëüïåðàòîðîì ñ
ðàâíîìåðíûì âðàùåíèåì öèëèíäðà. Ðîñò ýôôåê-
òèâíîñòè ÿâèëñÿ ñëåäñòâèåì óâåëè÷åíèÿ ïîäâèæ-
íîñòè ÷àñòèö ñåïàðèðóåìîé çåðíîñìåñè íà âèáðè-
ðóþùåé ðåøåòíîé ïîâåðõíîñòè öèëèíäðà. Òàê, ïðî-
õîäîâûå ÷àñòèöû (çåðíà), ïîïàäàþùèå íà ïåðå-
ìû÷êè ðåøåòà, ãðóáûå è êðóïíûå ïðèìåñè è îáðà-
çóþùèå ñâîäû íàä îòâåðñòèÿìè ïðè ðàâíîìåðíîì
âðàùåíèè öèëèíäðà ïåðåíîñÿòñÿ â ñõîä (îòõîäû).
Ïðè âðàùåíèè öèëèíäðà ñî çíàêîïåðåìåííûì
óñêîðåíèåì âñëåäñòâèå ïåðåìåùåíèÿ ÷àñòèö ñåïà-
ðèðóåìîé çåðíîñìåñè îòíîñèòåëüíî ðåøåòíîé ïî-
âåðõíîñòè óâåëè÷èâàåòñÿ âåðîÿòíîñòü ïðîñåèâàíèÿ
ïðîõîäîâûõ ÷àñòèö, ÷òî íà ïðàêòèêå âûðàæàåòñÿ â
óìåíüøåíèè ñîäåðæàíèÿ ãîäíîãî çåðíà â îòõîäàõ
(ñõîäå). Êðîìå òîãî, ïðèìåíåíèå âèáðàöèé ïîçâî-
ëèëî ðàñøèðèòü äèàïàçîí ðàçìåðîâ ïðèìåñåé, âûäå-
ëÿåìûõ èç çåðíà, ïóòåì óìåíüøåíèÿ ðàçìåðîâ îòâåð-
ñòèé ðåøåòíîé ïîâåðõíîñòè öèëèíäðà [1, 2] ïðè äî-
ïóñòèìîì ñîäåðæàíèè ïîëíîöåííîãî çåðíà â îòõîäàõ.
Òðåáîâàíèÿ ê êèíåìàòè÷åñêèì ïàðàìåòðàì ïðè-
âîäà ìîãóò áûòü ñôîðìóëèðîâàíû â ñëåäóþùåì âè-
äå: ïðèâîä äîëæåí îáåñïå÷èòü ñîîáùåíèå öèëèíäðó
53
ХРАНЕНИЕ И ПЕРЕРАБОТКА СЕЛЬХОЗСЫРЬЯ, № 1, 2014
ϕ
..
ϕ
0
ω
2
ϕ
.
ϕ
0
ω
1
0
1
0
–1
–1
Z
+
+
Z
+
-
π
π
2
2
π
3π
2
sin
δ
–cos
δ
δ
=
ω
t
δ
=
ω
t
δ
2+
δ
1+
δ
1+
+2
π
2
π
δ
*
+
π
a
á
Ðèñ. 2. Ãðàôè÷åñêàÿ èíòåðïðåòàöèÿ ðåøåíèÿ äèôôåðåíöè-
àëüíûõ óðàâíåíèé îòíîñèòåëüíîãî äâèæåíèÿ øêèâà: à – ãðà-
ôèê óñêîðåíèé; á – ãðàôèê ñêîðîñòåé
Электронная Научная СельскоХозяйственная Библиотека









