
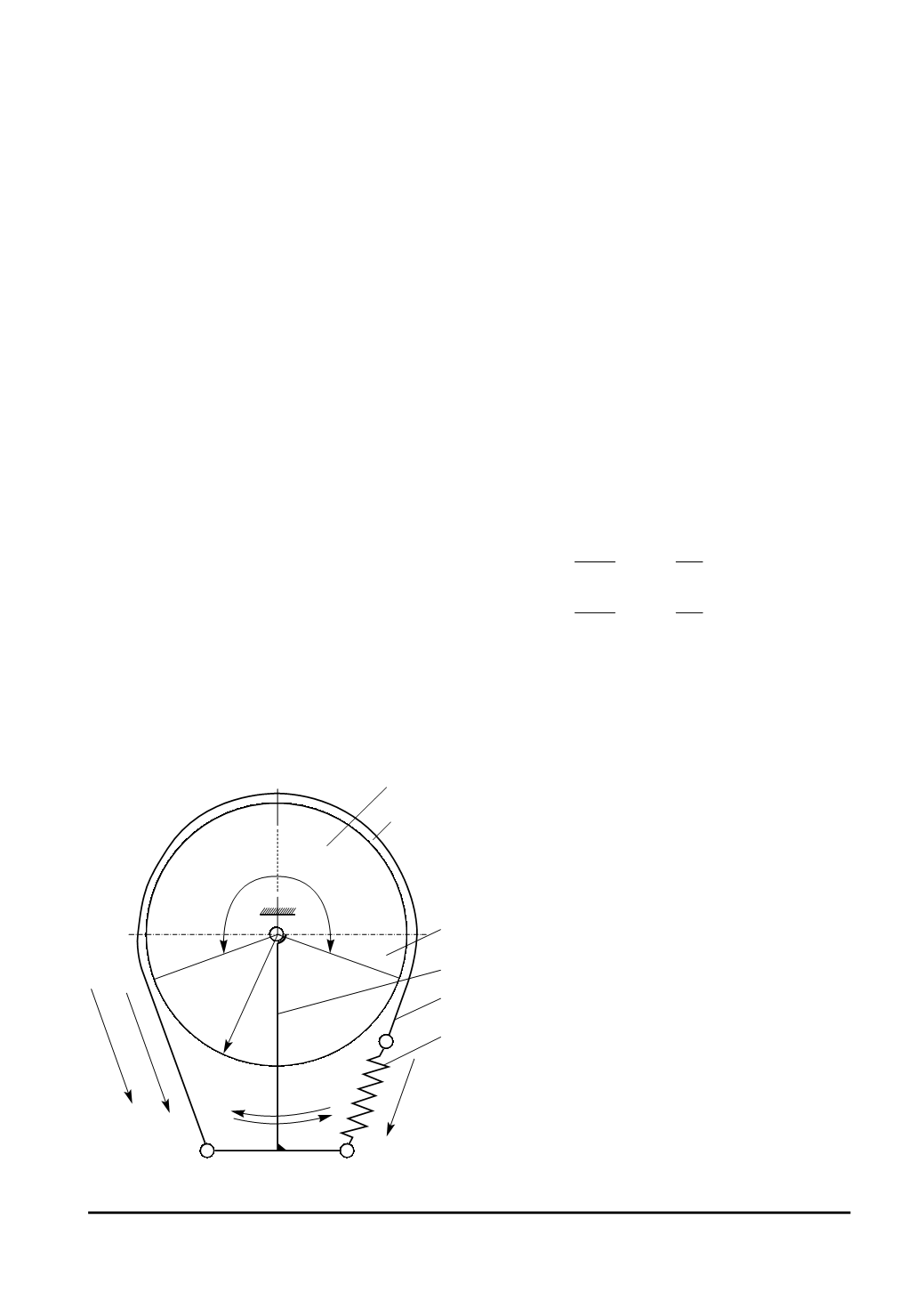
(ðèñ. 1), ïîçâîëÿþùèé ñîîáùèòü âûõîäíîìó çâåíó
âðàùåíèå ñ íàëîæåííûìè íà íåãî âðàùàòåëüíûìè
êîëåáàíèÿìè âîêðóã òîé æå îñè. Âûõîäíûì çâåíîì
ïðèâîäà ÿâëÿåòñÿ øêèâ
1
ðàäèóñà
R
ñ ïðèâåäåííûì
ìîìåíòîì èíåðöèè
I
, ñâîáîäíî âðàùàþùèéñÿ âî-
êðóã íåïîäâèæíîé îñè. Âõîäíîå çâåíî — ãèáêàÿ íå-
ðàñòÿæèìàÿ ëåíòà
2
, îáõâàòûâàþùàÿ áàðàáàí íà óãëå
α
è çàêðåïëåííàÿ íà òðàâåðñå
3
îäíèì êîíöîì æåñò-
êî, à äðóãèì — ÷åðåç óïðóãèé ýëåìåíò
4
. Òðàâåðñà
3
ñîâåðøàåò ãàðìîíè÷åñêèå âðàùàòåëüíûå êîëåáàíèÿ
ñ àìïëèòóäîé
ϕ
0
è ÷àñòîòîé
ω
ïî çàêîíó
ϕ
1
=
ϕ
0
sin
ω
t
îòíîñèòåëüíî îñè, ñîâïàäàþùåé ñ îñüþ âðàùåíèÿ
øêèâà, â ñèëó ÷åãî ïðåäâàðèòåëüíîå íàòÿæåíèå
S
0
óïðóãîãî ýëåìåíòà è äëèíà ëåíòû ïîñòîÿííû.
Ïðè êîëåáàíèÿõ òðàâåðñû æåñòêàÿ è ïîäïðóæè-
íåííàÿ âåòâè ëåíòû ïîî÷åðåäíî ÿâëÿþòñÿ ïî îòíî-
øåíèþ ê øêèâó âåäóùèìè, ò.å. â îäíîì ïîëóïåðèî-
äå êîëåáàíèé âåäóùåé ïî îòíîøåíèþ ê öèëèíäðó
ÿâëÿåòñÿ æåñòêàÿ âåòâü ëåíòû, à â äðóãîì — ïîäïðó-
æèíåííàÿ. Òàêèì îáðàçîì, íàòÿæåíèå
S
æåñòêîé
âåòâè ëåíòû â êàæäîì ïåðèîäå
Ò
= 2
π
/
ω
êîëåáàíèé
òðàâåðñû ïðèíèìàåò äâà çíà÷åíèÿ â çàâèñèìîñòè îò
íàïðàâëåíèÿ îòíîñèòåëüíîé ñêîðîñòè.
 ñîîòâåòñòâèè ñ ôîðìóëîé Ýéëåðà
S
1
=
S
0
e
α
f
è
S
2
=
S
0
e
-
α
f
,
ãäå
f
— êîýôôèöèåíò ñóõîãî òðåíèÿ ïàðû ëåíòà–øêèâ.
Ñîîòâåòñòâåííî è ìîìåíòû ñèë òðåíèÿ, ïðèëî-
æåííûå ê øêèâó ñî ñòîðîíû ëåíòû è âûçûâàþùèå
åãî äâèæåíèå, ðàçëè÷àþòñÿ â
e
α
f
ðàç. Ñëåäîâàòåëü-
íî, êàæäûé ïåðèîä êîëåáàíèé ñîäåðæèò èíòåðâàëû
âîçäåéñòâèÿ íà øêèâ ðàçëè÷íûõ ñèëîâûõ ôàêòîðîâ.
Èìååò ìåñòî àñèììåòðèÿ âîçáóæäåíèÿ, âûçûâàþ-
ùàÿ íàïðàâëåííîå â ñðåäíåì âðàùåíèå øêèâà ñî
ñðåäíåé óãëîâîé ñêîðîñòüþ
Ω
è çíàêîïåðåìåííûì
óñêîðåíèåì
ε
.
Èç âñåõ âîçìîæíûõ ðåæèìîâ äâèæåíèÿ øêèâà
íàèáîëåå ðàöèîíàëüíûì äëÿ ïðàêòè÷åñêîãî ïðè-
ìåíåíèÿ ÿâëÿåòñÿ ðåæèì, ñîäåðæàùèé èíòåðâàëû
ñîâìåñòíîãî äâèæåíèÿ øêèâà ñ ëåíòîé è ïðîñêàëü-
çûâàíèÿ åãî îòíîñèòåëüíî ëåíòû â íàïðàâëåíèè æå-
ñòêîé âåòâè. Â ýòîì ðåæèìå èìååò ìåñòî ìåíüøèé
èçíîñ ïàðû øêèâ–ëåíòà, òàê êàê ïðîñêàëüçûâàíèå
øêèâà îòíîñèòåëüíî ëåíòû ïðîèñõîäèò ïðè ñèëå
òðåíèÿ â ïàðå ìåíüøåé, ÷åì ïðè ïðîñêàëüçûâàíèè
øêèâà îòíîñèòåëüíî ëåíòû â íàïðàâëåíèè ïîäïðó-
æèíåííîé âåòâè.
Ïðè òåîðåòè÷åñêîì èññëåäîâàíèè ïðèâîäà àáñî-
ëþòíîå äâèæåíèå øêèâà ðàññìàòðèâàåòñÿ êàê ñóì-
ìà ïåðåíîñíîãî (äâèæåíèÿ âìåñòå ñ ëåíòîé) è îò-
íîñèòåëüíîãî (îòíîñèòåëüíî ëåíòû) ñêîëüæåíèÿ
øêèâà [1]. Ïðè ýòîì çà ïîëîæèòåëüíîå íàïðàâëå-
íèå êèíåìàòè÷åñêèõ è ñèëîâûõ ôàêòîðîâ ïðèíÿòî
èõ íàïðàâëåíèå îò ïîäïðóæèíåííîé âåòâè ëåíòû
ê æåñòêîé.
Äèôôåðåíöèàëüíîå óðàâíåíèå îòíîñèòåëüíîãî
äâèæåíèÿ øêèâà èìååò âèä [1]:
ϕ
..
=
ϕ
0
ω
2
(sin
δ
–
Z
+
),
(1)
ãäå
δ
=
ω
t
.
ãäå
Ì
ñ
— ìîìåíò âíåøíèõ ñèë ñîïðîòèâëåíèÿ âðà-
ùåíèþ øêèâà;
ϕ
2
— àáñîëþòíàÿ ñêîðîñòü øêèâà.
Çàìåòèì, ÷òî â ôîðìóëå (2) çíàê ìîìåíòà âíåø-
íèõ ñèë ñîïðîòèâëåíèÿ çàâèñèò îò íàïðàâëåíèÿ àá-
ñîëþòíîé ñêîðîñòè øêèâà. Â ðàáîòå [1] óñòàíîâëå-
íî, ÷òî åñëè
Z
+
+
> 0,217, òî ïðè ñêîëüæåíèè øêèâà
îòíîñèòåëüíî ëåíòû â ïîëîæèòåëüíîì íàïðàâëåíèè
àáñîëþòíàÿ ñêîðîñòü
ϕ
2
øêèâà è âíåøíèé ìîìåíò
ñîïðîòèâëåíèÿ
Ì
ñ
ìåíÿþò çíàêè. Ñëåäîâàòåëüíî, â
ýòîì ñëó÷àå ñêîëüæåíèå øêèâà îòíîñèòåëüíî ëåíòû
íà÷èíàåòñÿ ïðè çíà÷åíèè áåçðàçìåðíîãî ïàðàìåòðà
ñîïðîòèâëåíèÿ îòíîñèòåëüíîìó äâèæåíèþ, ðàâíîì
Z
+
+
, è ïîñëå èçìåíåíèÿ íàïðàâëåíèÿ
ϕ
2
ïðîäîëæàåò-
ñÿ ïðè çíà÷åíèè ýòîãî ïàðàìåòðà ðàâíîì
Z
+
-
. Åñëè
æå
Z
++
≤
0,217, òî àáñîëþòíàÿ ñêîðîñòü
ϕ
2
øêèâà è
âíåøíèé ìîìåíò ñîïðîòèâëåíèÿ
Ì
ñ
íå ìåíÿþò çíà-
êè, è ïðè îòíîñèòåëüíîì äâèæåíèè øêèâà áåçðàç-
ìåðíûé ïàðàìåòð îñòàåòñÿ ïîñòîÿííûì. Ïðè ýòîì
ôàçîâûé óãîë íà÷àëà îòíîñèòåëüíîãî ñêîëüæåíèÿ
øêèâà îïðåäåëÿåòñÿ èç óðàâíåíèÿ
δ
l+
= arcsin
Z
+
+
.
(3)
Ðåøåíèå âûïîëíåíî ìåòîäîì ïîýòàïíîãî èíòå-
ãðèðîâàíèÿ, îáîñíîâàííîãî â [4] ïðè èññëåäîâà-
íèè áåçîòðûâíîãî âèáðîïåðåìåùåíèÿ ïëîñêîé ìà-
òåðèàëüíîé ÷àñòèöû ïî øåðîõîâàòîé ïîâåðõíîñ-
òè, ñîâåðøàþùåé ïðÿìîëèíåéíîå ãàðìîíè÷åñêîå
êîëåáàíèÿ.
52
ХРАНЕНИЕ И ПЕРЕРАБОТКА СЕЛЬХОЗСЫРЬЯ, № 1, 2014
1
2
3
4
S
2
S
1
S
0
R
α
f
I
ϕ
0
sin
ω
t
Ðèñ. 1. Ñõåìà âèáðàöèîííîãî ïðèâîäà
f
0
c
2
2
0
0
f
0
c
2
2
0
0
1
ïðè 0;
1
ïðè 0,
RS
M
Z
e
I
RS
Z
RS
M
Z
e
I
RS
+
+
+
−
α
+
α
⎧
⎛
⎞
=
− +
ϕ >
⎪
⎜
⎟
ϕ ω
⎪
⎝
⎠
= ⎨
⎛
⎞
⎪ =
− +
ϕ <
⎜
⎟
⎪
ϕ ω ⎝
⎠
⎩
(2)
Электронная Научная СельскоХозяйственная Библиотека









