
5
•
2013
ПИВО
и
НАПИТКИ
27
ТЕХНОЛОГИЧЕСКИЕ ИННОВАЦИИ в ОТРАСЛИ
ТЕХНОЛОГИЧЕСКИЕ ИННОВАЦИИ в ОТРАСЛИ
ТЕМА НОМЕРА
В идеализированном виде про-
цесс экстрагирования в фильтре-
чане можно описать так. Снача-
ла полностью отделяют жидкую
фазу (первое сусло) объемом
V
Ж0
от твердой фазы. Затем осущест-
вляют
N
циклов, которые включа-
ют добавление некоторого объема
V
Ж
i
экстрагента (
i
-й промывной
воды), доведение до равновесия
концентраций компонента в твер-
дой и жидкой фазах, т. е. до вы-
полнения условия
a
i
=
Hc
i
, полное
отделение жидкой фазы объемом
V
Ж
i
от твердой и добавление вновь
отделенной жидкой фазы к ранее
отделенной.
Очевидно, что в таком процес-
се объем твердой фазы
V
Т0
не из-
меняется. Концентрация компо-
нента в твердой фазе изменяется
от
a
0
до
a
N
. Остаточная концентра-
ция компонента в твердой фазе
a
N
определяет степень извлечения
E
ФЧ
компонента в фильтре-чане
из исходного затора.
(
V
T0
a
0
+
V
Ж0
c
0
) –
V
T0
a
N
E
ФЧ
= ————————————, (2)
V
T0
a
0
+
V
Ж0
c
0
где в числителе масса компонента,
извлеченная из затора, т. е. оказав-
шаяся в экстракте, а в знаменате-
ле — исходная масса компонента,
находившаяся в заторе. После не-
сложных преобразований, учитывая
(1), получим
V
T0
/
V
Ж0
a
N
E
ФЧ
= 1 – ———————— ——. (3)
1/
H
+
V
T0
/
V
Ж0
a
0
Теперь определим концентрацию
экстракта
c
Э
, получаемую при за-
данной степени извлечения, т. е.
заданной остаточной концентрации
a
N
в твердой фазе:
(
V
T0
a
0
+
V
Ж0
с
0
) –
V
T0
a
N
c
Э
= ————————————. (4)
V
Ж0
+
Σ
N
i
= 1
V
Ж
i
В уравнении (4) в числителе мас-
са компонента, оказавшаяся в экс-
тракте, а в знаменателе — сум-
марный объем экстракта, который
складывается из объема жидкой
фазы исходного затора и
N
объемов
промывных вод.
Рассмотрим баланс массы ком-
понента на (
i
–1)-м и
i
-м циклах до-
бавления экстрагента (промывных
вод):
V
T0
a
i
–1
=
V
T0
a
i
+
V
Ж
i
c
.
(5)
Учитывая, что
a
i
=
Hc
i
, после
преобразований получим
a
i
–1
–
a
i
V
Ж
i
=
V
T0
H
—————.
(6)
a
i
Определим безразмерную кон-
центрацию компонента в твердой
фазе в виде
a
i
A
i
= —,
i
= 0, ...,
N
.
(7)
a
0
Тогда уравнение (6) можно запи-
сать следующим образом:
V
Ж
i
A
i
–1
–
A
i
—— =
H
—————.
(8)
V
T0
A
i
Соотношение (4) также можно
записать в безразмерном виде
с
Э
1 +
H
(
V
T0
/
V
Ж0
) (1 –
A
N
)
—— = ————————————. (9)
c
0
1+
Σ
N
i
= 1
(
V
Ж
i
/V
Ж0
)
Очевидно, что для любого случая
A
0
= 1, а
A
N
определяется заданной
степенью извлечения согласно (3),
причем 0 <
A
N
< 1. Поэтому отно-
сительная концентрация экстракта
c
Э
/
с
0
согласно (9) и (8) являет-
ся функцией (
N
– 1) переменных
A
1
, …,
A
N
–1
.
Заметим, что все промежуточ-
ные значения безразмерных кон-
центраций компонента в твердой
фазе
A
i
лежат внутри отрезка от
A
N
до
A
0
=1, причем
0<
A
N
<
A
N
–1
<…<
A
i
<…<
<
A
2
<
A
1
< (
A
0
=1).
(10)
Таким образом, для любого
процесса вне зависимости от кон-
кретных размерных значений на-
чальных и конечных концентра-
ций компонента безразмерные
величины
A
i
ограничены согласно
(10). Следовательно, если задаться
некоторым малым шагом
δ
A
изме-
нения концентраций
A
i
от
A
N
до 1,
мы получим ограниченный набор
возможных
A
i
,
i
= 1, …,
N
–1. На-
пример, в случае трех промывных
вод (
N
= 3) мы будем иметь огра-
ниченный набор пар
A
1
и
A
2
.
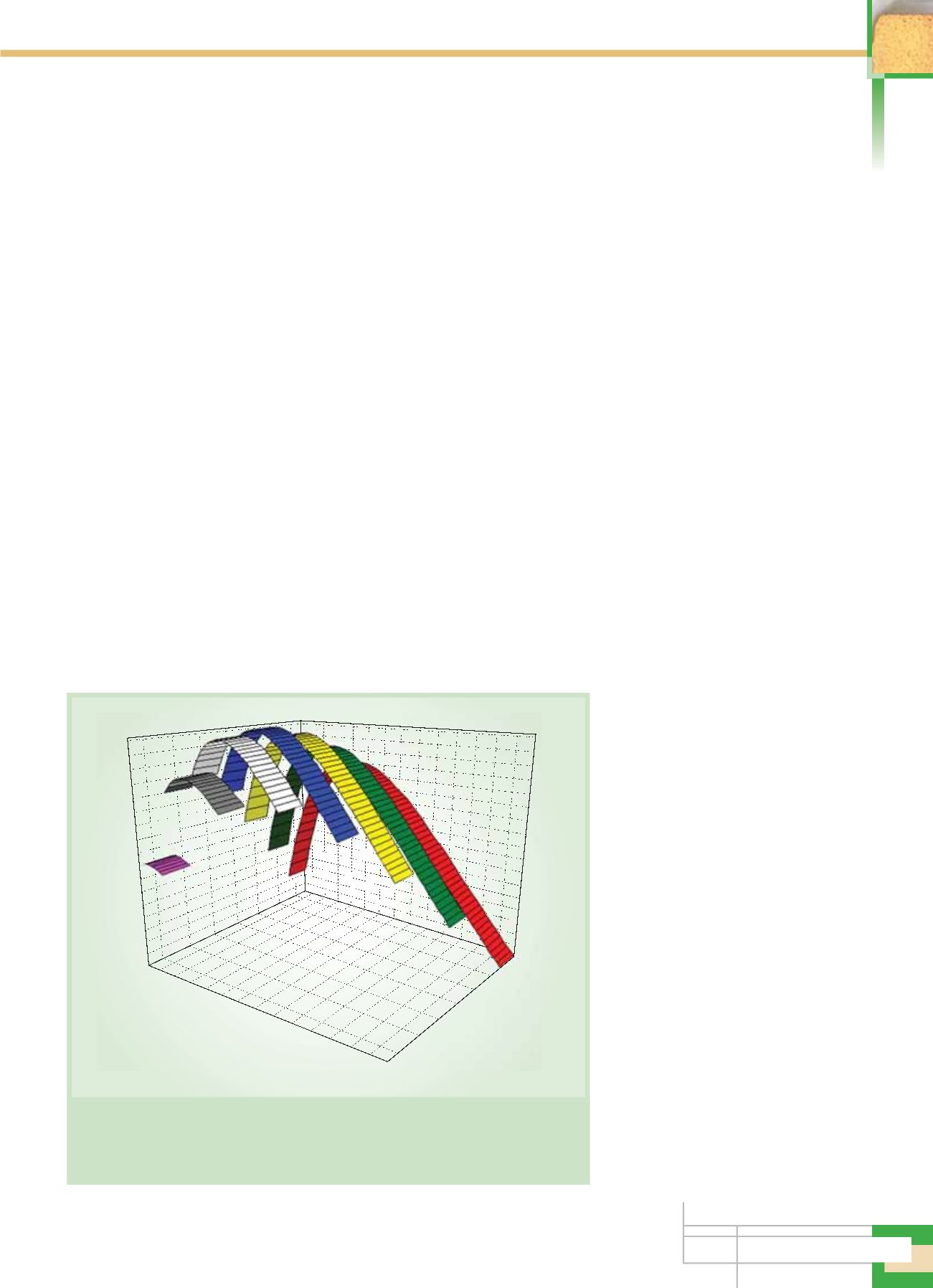
Рис. 1.
Зависимость относительной концентрации экстракта
от промежуточных концентраций
A
1
и
A
2
.
Число промывных вод
N
= 3, степень извлечения
E
ФЧ
= 0,94 (
A
N
= 0,2),
H
= 1,
V
T0
/
V
Ж0
= 3/7
C
Э
0,25
0,35
0,45
0,55
0,65
0,75
0,85
0,3
0,4
0,5
0,6
0,7
0,8
0,9
0,7
0,69
0,68
0,67
0,66
0,65
0,64
0,63
0,62
0,61
0,60
0,59
0,58
0,57
0,56
0,55
0,54
А
2
А
1
Электронная Научная СельскоХозяйственная Библиотека









