ЭлБиб

ПИЩЕВАЯ ПРОМЫШЛЕННОСТЬ

11/2005

ТЕХНИКА И ТЕХНОЛОГИЯ

Задача снижения энергозатрат при

использовании теплового и холодиль(

ного оборудования возникает как на

стадии определения наиболее энерге(

тически эффективного процесса, так и

при создании, оценке или модерниза(

ции аппарата, позволяющего реализо(

вать выбранный процесс. Учитывая ог(

ромные объемы обрабатываемой про(

дукции и непрерывный рост стоимости

энергоресурсов, выбор энергетически

эффективных процессов и аппаратов

представляет немалый интерес.

Для решения этой задачи предлага(

ется использовать безразмерный кри(

терий энергетической эффективности,

дающий качественную оценку как кон(

кретного теплового процесса в отдель(

ности, так и процесса в совокупности с

соответствующим оборудованием.

Безразмерный критерий L представ(

Безразмерный критерий

энергетической эффективности

тепловых процессов и аппаратов

А.А. Гажур

Российская экономическая академия им. Г.В. Плеханова

ляет собой отношение энергозатрат,

обеспечивающих протекание суще(

ствующего практически процесса Q к

минимально теоретически возможным

энергозатратам Qmin и позволяющих

соблюсти все предъявляемые к конеч(

ному состоянию продукта биохимичес(

кие и органолептические требования

L = Q/Qmin .

Чем ближе величина критерия L к

единице, тем выше качество рассмат(

риваемого процесса или аппарата, ре(

ализующего этот процесс.

Энергозатраты на процесс Q включа(

ют в себя затраты энергии при стацио(

нарном и нестационарном режимах, а

также приведенные капитальные зат(

раты, выраженные в энергетических

единицах. Затраты на стационарный

режим (проведение процесса) состоят

из затрат на изменение (или сохране(

ние) температурного поля в продукте,

а также из потерь от контакта с окружа(

ющей средой. Затраты на нестационар(

ный процесс складываются из затрат

при выходе аппарата на стационарный

режим, включающих затраты на разог(

рев (охлаждение) конструкции аппа(

рата, и, соответственно, потерь от кон(

такта с окружающей средой в течение

нестационарного процесса.

В результате получаем многопара(

метрическое уравнение, где независи(

мыми переменными являются характе(

ристики процесса (задаваемые началь(

ное и конечное распределения темпе(

ратуры в продукте и длительность про(

цесса или их допустимые диапазоны

изменения), характеристики продукта

(коэффициенты теплопроводности,

теплоемкости и т. д.), характеристики

аппарата (например, параметры ог(

раждения), эксплуатационные харак(

теристики (количество рабочих цик(

лов) и варьируемые параметры, влия(

ющие на величину приведенных капи(

тальных затрат (например, величина

толщины слоя теплоизолирующей час(

ти ограждения).

Поставленной таким образом задаче

удовлетворяет n(мерное пространство

решений, каждой точке которого соот(

ветствует какой(либо допустимый про(

цесс и реализующий его возможный

аппарат.

В целях получения графической ин(

терпретации можно упростить уравне(

ние, приняв часть переменных величин

за постоянные. Рассмотрим, например,

процесс тепловой обработки, описыва(

емый условиями Дирихле, чему соот(

ветствует контактный нагрев. В каче(

стве переменных величин оставим ха(

рактеристику источника Тс – величину

температуры, поддерживаемой на по(

верхности продукта в течение процесса

и величину толщины теплоизолирую(

щего слоя ограждения

. В качестве

объекта нагрева возьмем элемент нео(

граниченной пластины XxYxZ, поме(

щенный между поверхностями, на ко(

торых поддерживается постоянная

температура Тс (источниками) и слоя(

ми ограждения, толщиной

каждый.

Зададимся начальным распределени(

ем температуры в продукте (Тн), диа(

пазонами допустимых конечных темпе(

ратур (Тmin< Tk <Tmax) и длительнос(

ти процесса (

min <

max), а также

физическими характеристиками про(

дукта (плотностью

, коэффициентами

теплопроводности

и теплоемкости

), ограждения (

, с

), температу(

рой окружающей среды Токр, средней

приведенной стоимостью аналогично(

го оборудования Qкап и количеством

рабочих циклов n. В качестве теорети(

чески минимальных энергозатрат Qmin

возьмем энергозатраты при конечном

распределении Tk = Тmin.

Подставим в решение задачи следу(

ющие конкретные значения: Х = 0,02

м, Y= Z = 1 м, Тн = 293

К, 333

К < Tk <

383

К, 200 c <

< 800 c,

= 800 кг/м

= 20 кг/м

= 0,197Дж/(мсК),

= 0,046 Дж/(мсК), с

= 1760 Дж/

(кгК), с

= 922 Дж/(кгК), Токр = 293

К,

Qкап = Qmin, n = 36.

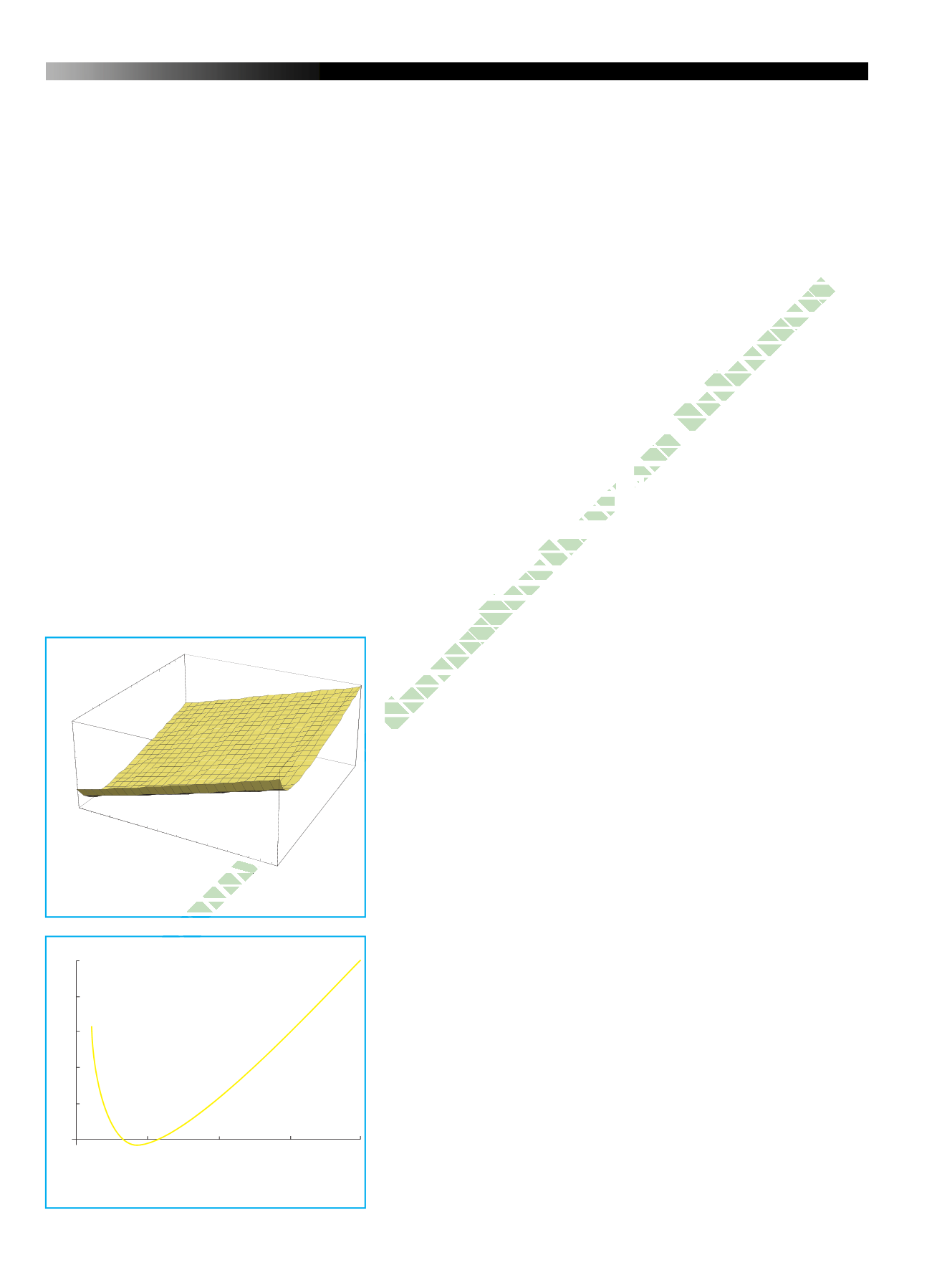
Результат вычислений показан на

рис. 1. Получаем поверхность, состоя(

щую из бесконечного множества про(

цессов и соответствующих им аппара(

тов, удовлетворяющих поставленным

условиям. Анализируя эту поверх(

ность, можем выбрать энергетически

эффективные процесс и аппарат. При(

ведем на рис. 2. сечение этой поверх(

ности плоскостью, перпендикулярной

оси температур источника в точке Тс =

363

К. Это соответствует случаю, когда

процесс выбран (Тс = 363

К) и требу(

ется подобрать наиболее энергетичес(

ки эффективное оборудование для его

осуществления. Вид функции, отобра(

женной на рис. 2, показывает наличие

минимума, которому и соответствует

наиболее энергетически эффективный

аппарат.

Проведение такой оценки качества

можно остановить на той стадии, кото(

рая представляет интерес: оценка и

выбор процесса, аппарата, процесса и

аппарата, выяснить зависимость опти(

мальных показателей от длительности

суточной работы оборудования и т. д.

При внедрении такой системы можно

каждый аппарат сертифицировать на(

бором чисел, каждое из которых пока(

зывает его энергетическую эффектив(

ность по отношению к реализуемым

этим аппаратом тепловым процессам.

Рис. 1. Поверхность процессов и аппаратов (зависимость

безразмерного критерия энергетической эффективности L

от температуры источника Тс и толщины ограждения

)

350 360 370 380

, м

Тс, °К

0,05 0,1 0,15 0,2

2,8

2,6

2,4

2,2

Рис. 2. Сечение поверхности процессов и аппаратов

(линия аппаратов). Температура источника Тс = 363 °К

2,65

2,6

2,55

2,5

2,45

0,05 0,1 0,15

, м

Электронн

ая Научна

я СельскоХозяйственная Библиотека