к этим фракциям кривые пересекаются кривыми, относящимися к более
мелким фракциям.
При этом оказывается, что отдельные участки кривых, особенно на-
чальные, по своей форме весьма близки к параболам. Это не трудно пока-
зать следующим путем. Общей формулой для кривых параболического
типа является следующая:
х = ку
п
.
Логарифмируя это выражение, получаем:
lgx=lgk
+nlgy.
Это последнее уравнение линейное. Следовательно, если мы разместим
в системе прямоугольных координат точки, соответствующие некоторым
парным значениям lg
t
и
IgA, и эти точки лягут на
прямую линию, то мы мо-
жем счесть это за доказа-
тельство того, что иссле-
дуемая кривая действи-
тельно имеет параболиче-
скую форму.
Применив этот метод к
кривым, изображенным на
рис. 79, мы построили гра-
фики зависимости
l g A - / ( l g . O .
где
h
— высота подъема
в см;
t
—время в часах.
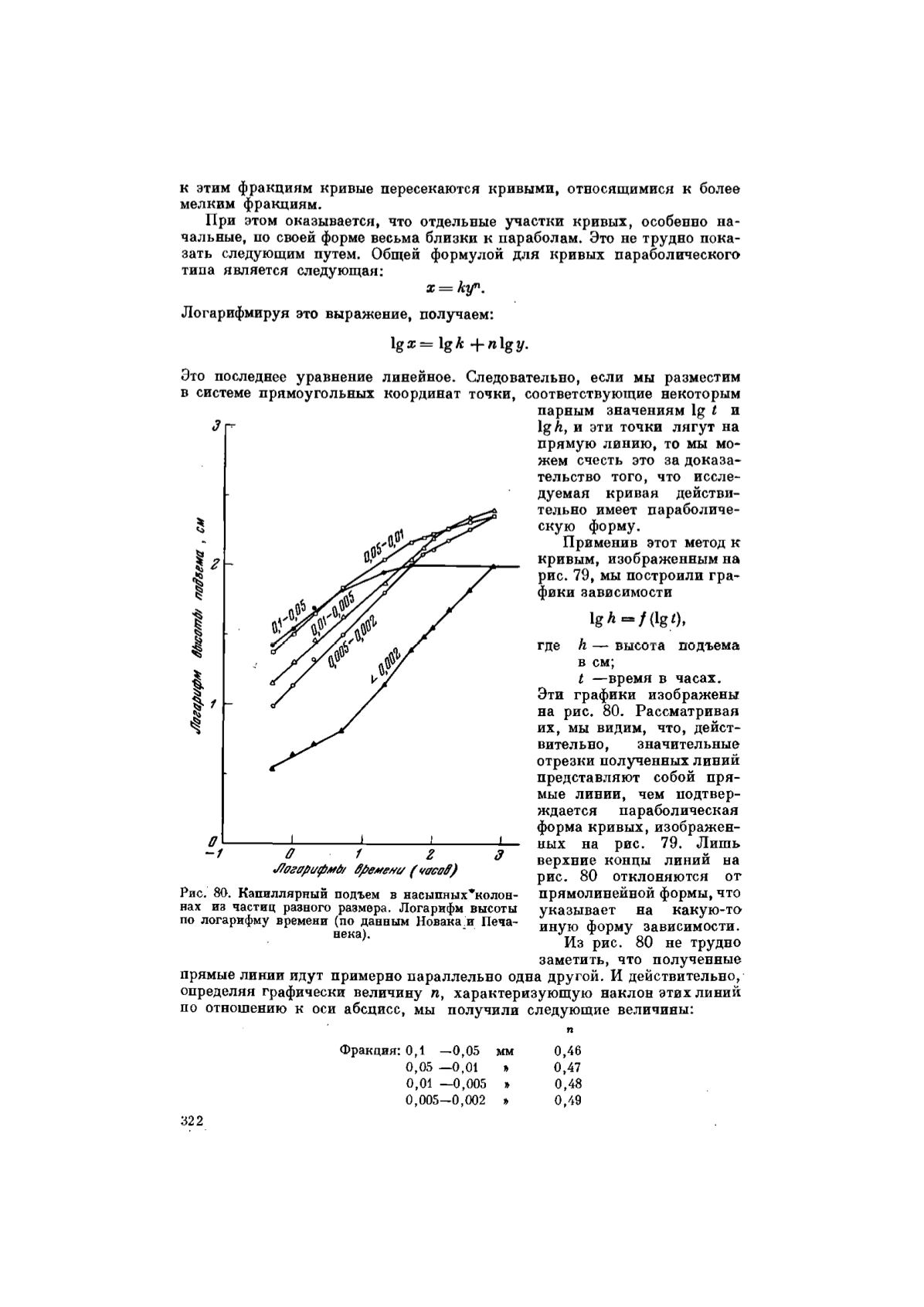
Эти графики изображены
на рис. 80. Рассматривая
их, мы видим, что, дейст-
вительно ,
значительные
отрезки полученных линий
представляют собой пря-
мые линии, чем подтвер-
ждается параболическая
форма кривых, изображен-
ных на рис. 79. Лишь
верхние концы линий на
рис. 80 отклоняются от
прямолинейной формы, что
указывает на какую-то
иную форму зависимости.
Из рис. 80 не трудно
заметить, что полученные
прямые линии идут примерно параллельно одна другой. И действительно,
определяя графически величину
п
у
характеризующую наклон этих линий
по отношению к оси абсцисс, мы получили следующие величины:
п
Фракция: 0,1 —0,05 мм
0,46
0,05 —0,01
ь
0,47
0,01 —0,005 »
0,48
0,005-0,002
»
0,49
I'
1
!
_
1
I
I
1
—/
о - 1
z
д
</7аг0рифм6/ времени (vaceff)
Рис. 80. Капиллярный подъем в насыпных^колон-
нах из частиц разного размера. Логарифм высоты
по логарифму времени (по данным Новака и Печа-
нека).
322»
Электронная книга СКБ ГНУ Россельхозакадемии


