
Научный журнал Российского НИИ проблем мелиорации, № 3(11), 2013 г., [125-133]
4
ω
r
φ·r
2π·r
β
А
А
1
h
h
/
В
С
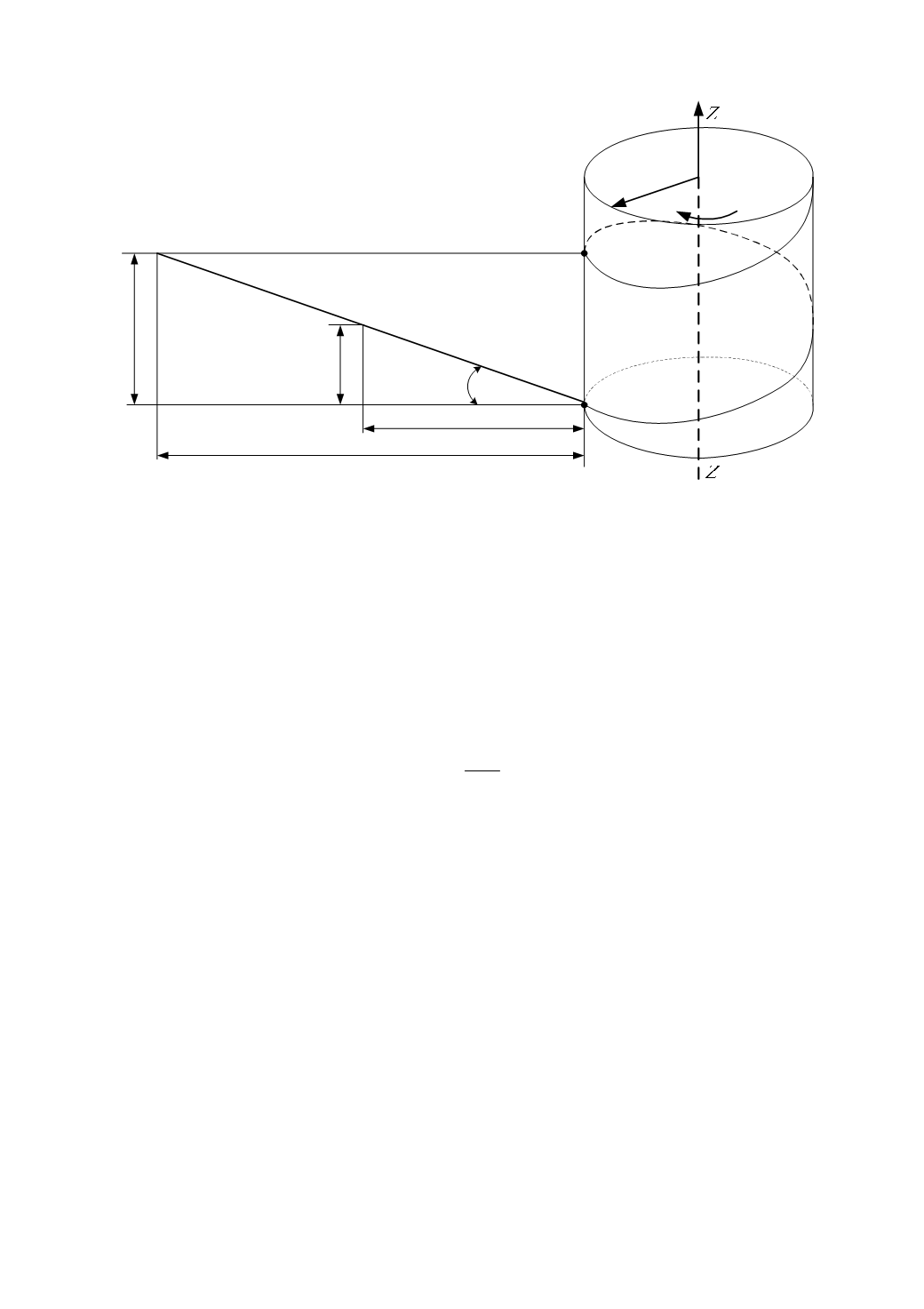
Рисунок 3 – Винтовая линия шнека и ее развертка на плоскость
Соотношение (4) налагает связь на движение пары винтовой линии
шнека и точки
А
вдоль и вокруг оси
Z-Z
. Если шнек повернуть на полный
оборот (угол, равный
2π
), то точка
А
переместится вдоль оси
Z-Z
на вели-
чину
h
, которая называется шагом винтовой линии [2]. Так как из тре-
угольника
В А С
следует, что:
,
π2
tgβ
r
h
откуда находим
h
шаг винтовой линии шнека:
tgβ π2
r h
,
(5)
где
r
– радиус цилиндра, на котором расположена винтовая линия шнека;
β
– угол подъема винтовой линии.
Так как
t
ω
, а
b
– величина перемещения точки
a
вдоль оси
Z-Z
в положение
a
за время
t
при повороте шнека на угол
, равная
π2/ ω/
h
b
(рисунок 4), то для нахождения длины одного витка винто-
вой линии уравнения (1), (2) и (3) винтовой линии в декартовой системе
координат
X Y Z
, представим в следующем виде:
Электронная Научная СельскоХозяйственная Библиотека









