
278
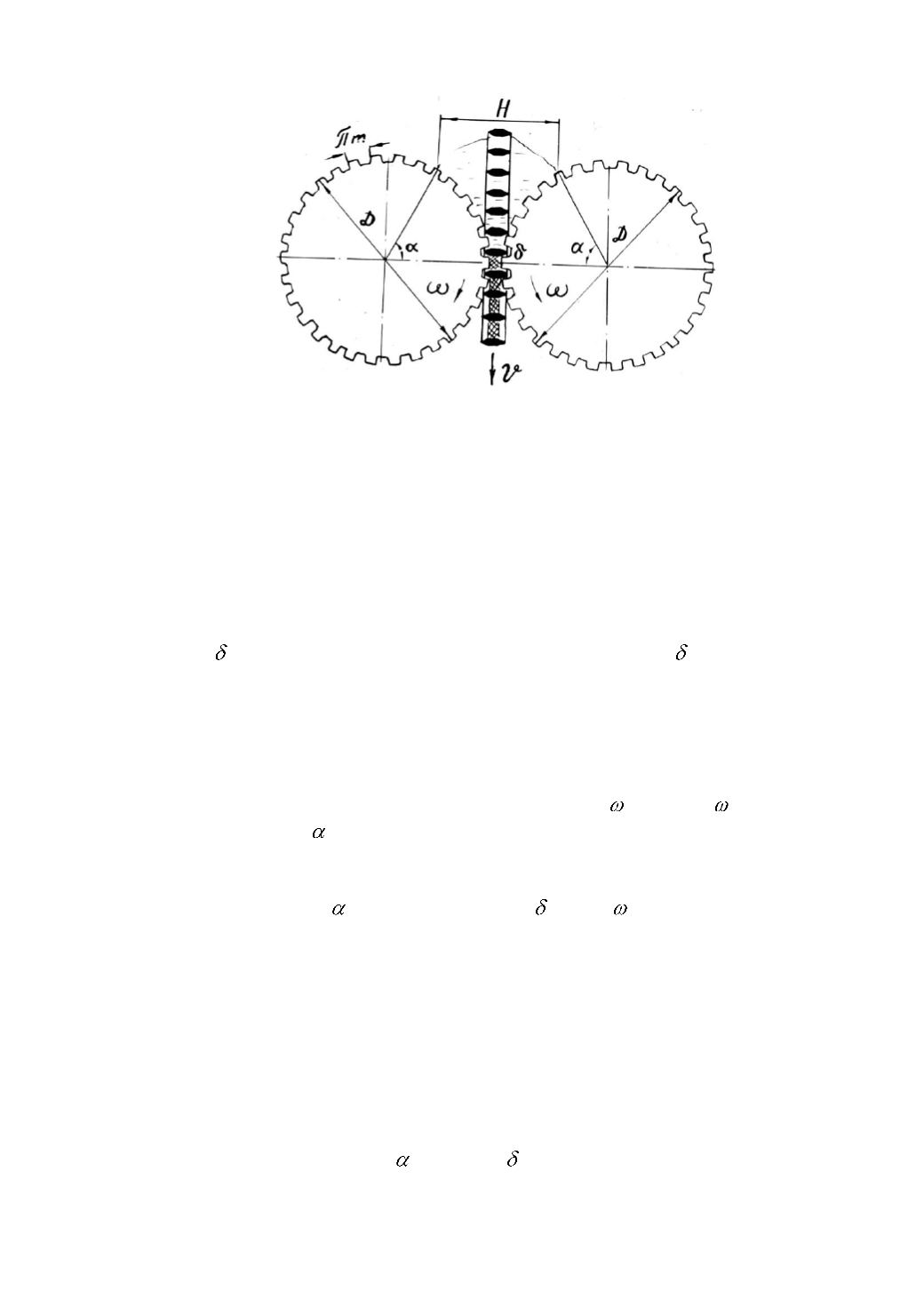
Рисунок 6.4 – Схема к определению угла захвата кормовой смеси
рабочим органом шестерѐнного пресса формующего типа
Уравнения размерностей примут вид:
L: a + b – 3c = 0,
M: c = 0,
T: -d = 0.
Решение однозначно:
а = - b
. Безразмерный комплекс примет вид
m/D
.
Аналогично для ширины колес
В (L)
, длины частиц
l (L)
и зазора между
зубьями
(L)
получим безразмерные комплексы
В/D
, l/D,
/D
.
Для ускорения свободного падения
g (LT
-2
)
уравнения размерностей
(LT
-2
)
a
(L)
b
(ML
-3
)
c
(T
-1
)
d
= M
0
L
0
T
0
, (6.4)
a + b – 3c = 0, a = - b,
-3c = 0,
-2a – d = 0, d = - 2a
.
Безразмерный комплекс принимает вид
g
a
/D
a a2
или
g/D
2
.
Факторы
f
и , являющиеся безразмерными величинами, приводятся к
виду симплексов.
Тогда критериальное уравнение примет вид:
= F( m/D; B/D; l/D; /D; g/D
2
;f )
. (6.5)
Отношение четвертого члена ко второму характеризует размеры зоны
сжатия и является критерием геометрического подобия. Первый и третий
комплексы также характеризуют геометрическое подобие зубчатых колес
[88, 89]. Два последних члена критериального уравнения характеризуют из-
менение условий проявления сил тяжести и трения. Ввиду того, что захваты-
вающая способность рассматривается при установившемся движении в не-
значительном диапазоне возможного изменения угловой частоты только
стальных колес, существенно влиять на угол захвата они не могут.
Критериальное уравнение теперь примет вид:
= C(m/D; /B; l/D).
(6.6)
Элек ронная Научная СельскоХозяйственная Библиотека









