
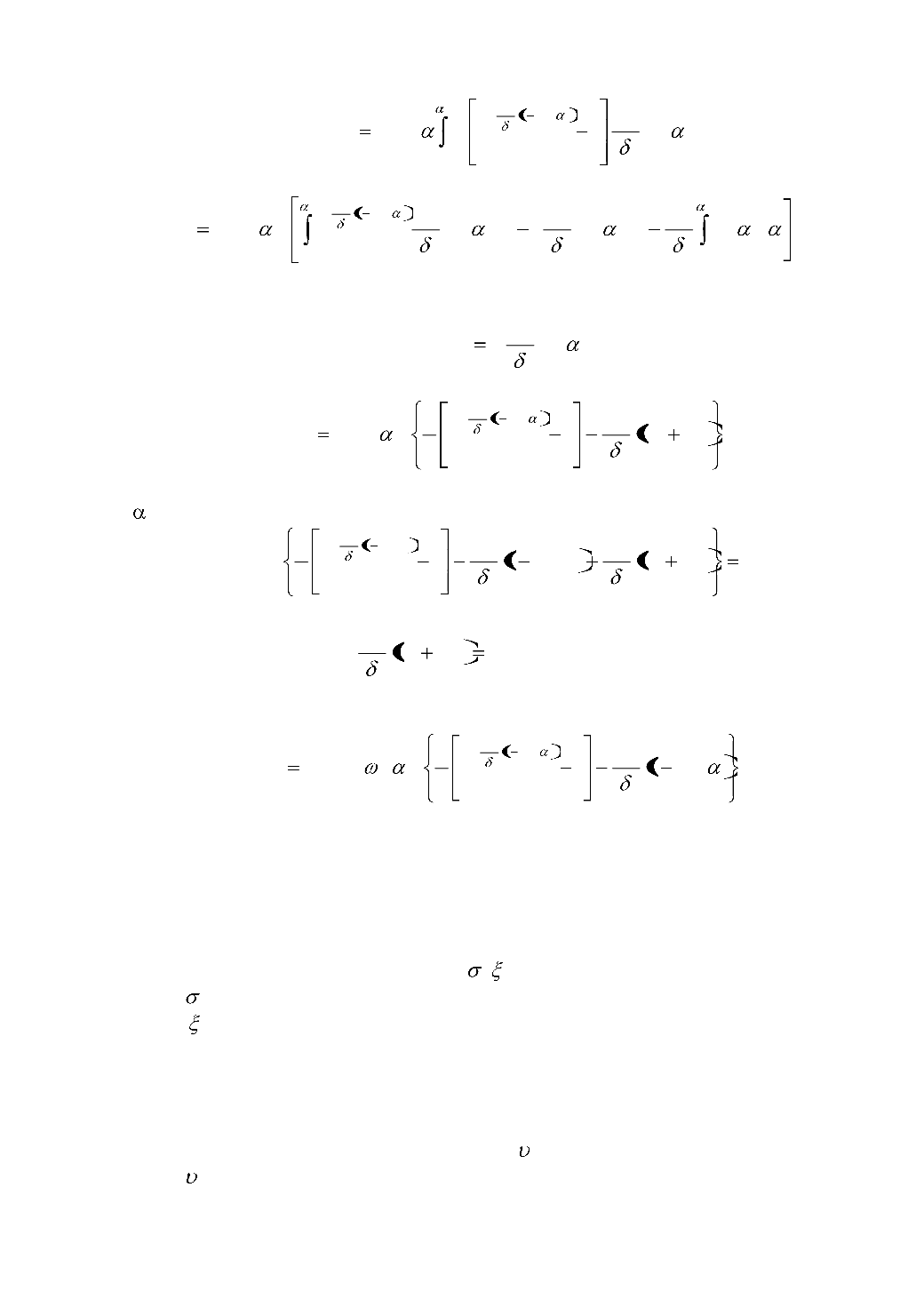
282
0
cos 1
2
0
1
sin
2
1
dα
R
eP BRk N
R
a
. (6.28)
Преобразуя его, получим
0
0
cos 1
2
0
1
sin
2
sin
2
1
sin
2
d
R
dα
R
dα
R
e P BRk N
R
a
. (6.29)
Обозначив показатель экспоненты через
х
, определим его дифференци-
ал:
sin
2
R
a dx
. (6.30)
Решением (6.29) будет:
1
2
cos 1
2
0
1
2
1
1
C C
R
e
a
PBRk N
R
a
. (6.31)
Для определения постоянных интегрирования рассмотрим случай при
=0, когда нормальные силы отсутствуют. При этом
0
2
0 cos 1
2
1
1
2
1
0 cos 1
2
CC
R
R
e
a
R
a
, (6.32)
отсюда
0
2
2
1
CC
R
или
С
1
+ С
2
= 0
. (6.33)
Следовательно, необходимая мощность для сжатия кормовой смеси
зубчатыми колесами, будет равна:
cos 1
2
1
1
2
cos 1
2
0
2
1
R
e
a
PB fRk
N
R
a
сж
. (6.34)
Мощность холостого хода пресса зависит от конструкции передач в
трансмиссии и определяется экспериментально [83, 86, 102, 133].
Мощность на выталкивание брикетов из камер обуславливается пре-
одолением сил трения при перемещении до выхода из камер. При этом силы
трения определяются не только приложенным давлением, но и остаточным
боковым давлением сил упругих деформаций [86].
F = (
r
+ q
0
)Uh
, (6.35)
где
r
– напряжение в точках брикета, прилегающих к стенкам камеры;
– коэффициент бокового давления;
q
0
– остаточное боковое давление;
U
– периметр камеры прессования;
h
– высота брикета.
Мощность на выталкивание брикетов будет равна:
N
в
= F ,
(6.36)
где – относительная скорость выталкивателя.
Электронная Научная СельскоХозяйственная Библиотека









