
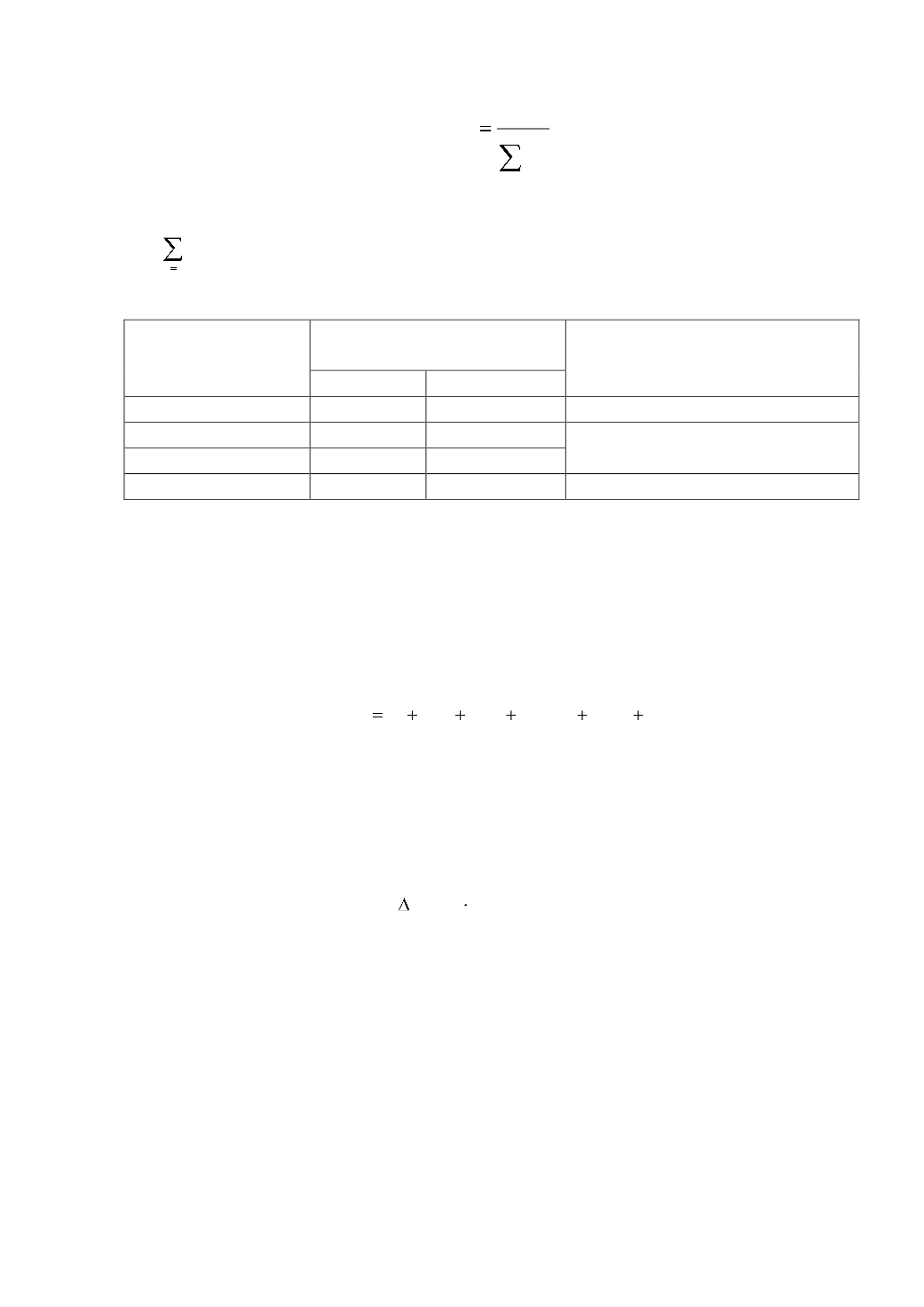
211
,
max
n
1
2
u
2
u
p
S
S
G
(4.61)
где
2
u
S
max
– максимальная построчная оценка дисперсии из всех 9-ти опытов в
плане;
– сумма оценки дисперсии для всех 9-ти опытов в эксперименте.
Таблица 4.2 – Ортогональный план двухфакторного эксперимента
№ п/п
Уровни факторов
в опыте
Критерий
оптимизации (
у
)
Х
1
Х
2
1–4
±1
±1
Ядро эксперимента
5–6
±1
0
Звездные точки
7–8
0
±1
9
0
0
Нулевая точка
Расчетное значение критерия Кохрена должно быть меньше теоретиче-
ского (табличного) для установленного уровня значимости результата.
В эксперименте принята надежность результатов не ниже 0,95 (уровень
значимости 0,05).
После подтверждения воспроизводимости опытов рассчитывали коэф-
фициенты уравнения регрессии, которые для каждого критерия оптимизации
в общем виде являются полиномом второго порядка:
2
2 22
2
1 11
21 12
22 11
0
хв хв ххв хв хв в y
, (4.62)
где
у
– критерий оптимизации (производительность или крошимость гранул
в принятых трех вариантах комплектации гранулятора);
0
в
,
1
в
,
2
в
,
11
в
,
22
в
– численные коэффициенты уравнения;
1
х
,
2
х
– обозначения закодированных факторов.
Значимость коэффициентов уравнения статистически проверялась по
доверительному интервалу каждого из них:
i
b
=±
и
St
,
(4.63)
где
t
– критерий Стьюдента для принятого уровня значимости и соответ-
ствующего числа степеней свободы [20, 116];
и
S
– среднеквадратичное отклонение оценки дисперсии.
Окончательная адекватность расчетных по уравнению значений крите-
рия оптимизации и полученных значений в опытах проверялась по критерию
Фишера (по компьютерной программе на
Ф
-тест).
Статистические проверенные уравнения регрессии представляли мате-
матическую модель процесса. Полная модель представляла систему двух
уравнений: первого – для количественного критерия оптимизации и второго
– для качественного.
и
1п
2
п
S
Электронная Научная СельскоХозяйственная Библиотека









