
163
Координаты центра поверхности, соответствующие максимальному
значению критерия оптимизации, находятся по первым производным функ-
ции (3.41):
-1,98 + 0,13х
2
+ 0,61х
3
+ 0,2х
1
= 0;
1,40 + 0,13х
1
– 1,13х
3
+ 1,12х
2
= 0; (3.42)
-0,86 + 0,61х
1
–1,13х
2
+ 2,46х
3
= 0.
Решением этого уравнения определены координаты центра этой по-
верхности: х
1
= – 19,31, х
2
= 5,64, х
3
= 5,6.
Значения факторов, соответствующие центру поверхности, являются
технически невыполнимыми, поэтому наиболее близкими к оптимальным
приняты значения факторов: х
1
= –1; х
2
= 1; х
3
=1.
Для анализа взаимного влияния факторов необходимо воспользоваться
уравнением в раскодированном виде:
φ = 38,30 – 0,04505·D + 0,5425·m – 1,828·α + 0,2708·10
–3
·D·m +
+0,00101·D·α – 0,0565·m·α + 0,694·10
-5
·D
2
+ 0,035·m
2
+ 0,0492·α
2
. (3.43)
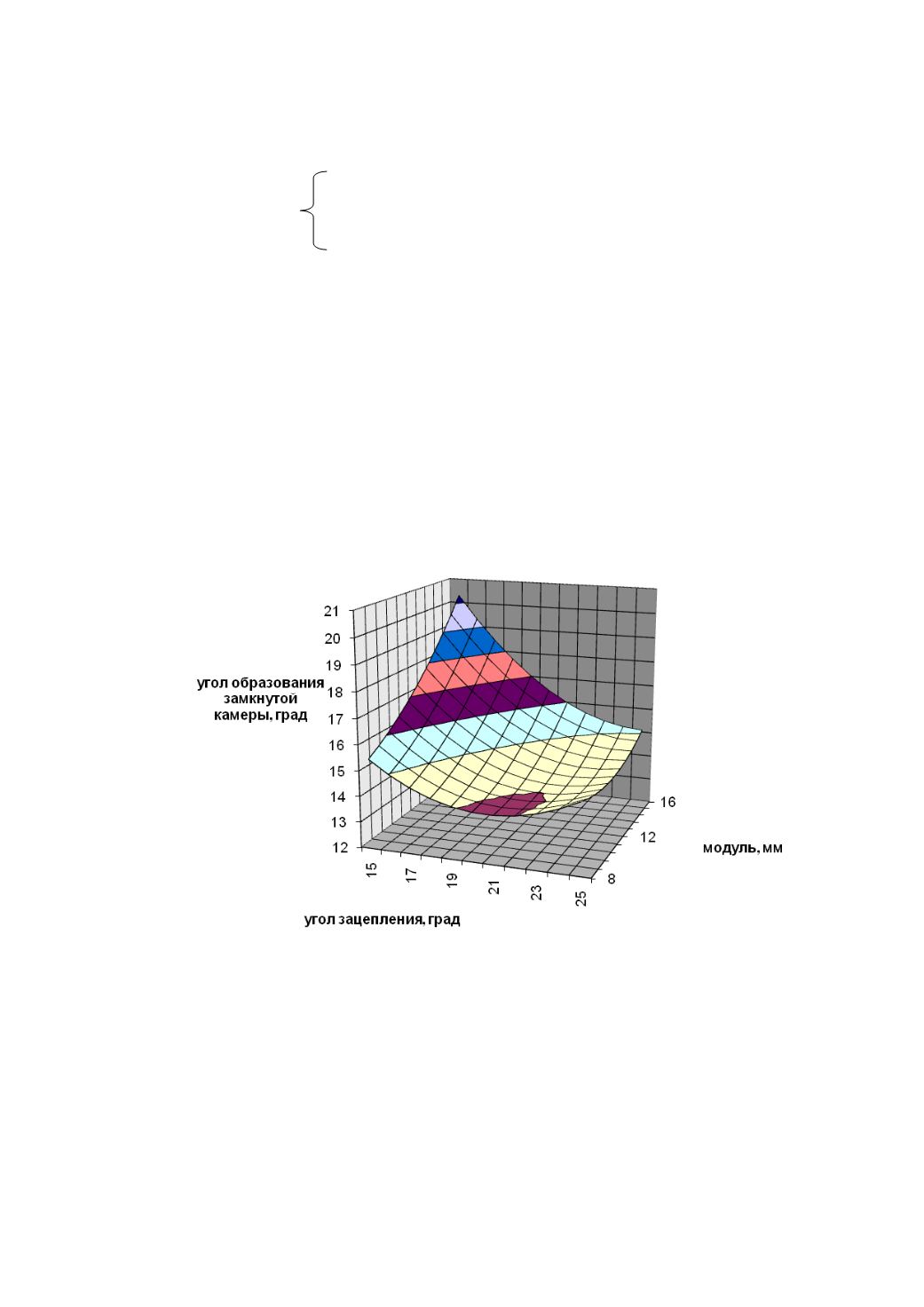
Для наглядного представления влияния факторов на критерий оптими-
зации необходимо воспользоваться графиком поверхности отклика при фик-
сации одного параметра (рисунок 3.12).
Рисунок 3.12 – Поверхность отклика
(делительный диаметр зубчатого колеса – 240 мм)
Критерий оптимизации увеличивается при увеличении модуля и
уменьшается при средних значениях угла зацепления.
Оптимальной зоной можно признать соотношение значений модуля от
15 до 16 мм и угла зацепления от 15 до 17 градусов.
Поверхность отклика влияния угла зацепления и диаметра делительной
окружности колеса на критерий оптимизации представлен на рисунке 3.13.
Электронная Научная СельскоХозяйственная Библиотека









