
39
;
cos
2
1
2
4
L
Y
(2.7)
,
sin
sin
2
4
3
1
2
L
Z
(2.8)
где
L
– яркость прямоугольника CDFG (рисунок 2.2).
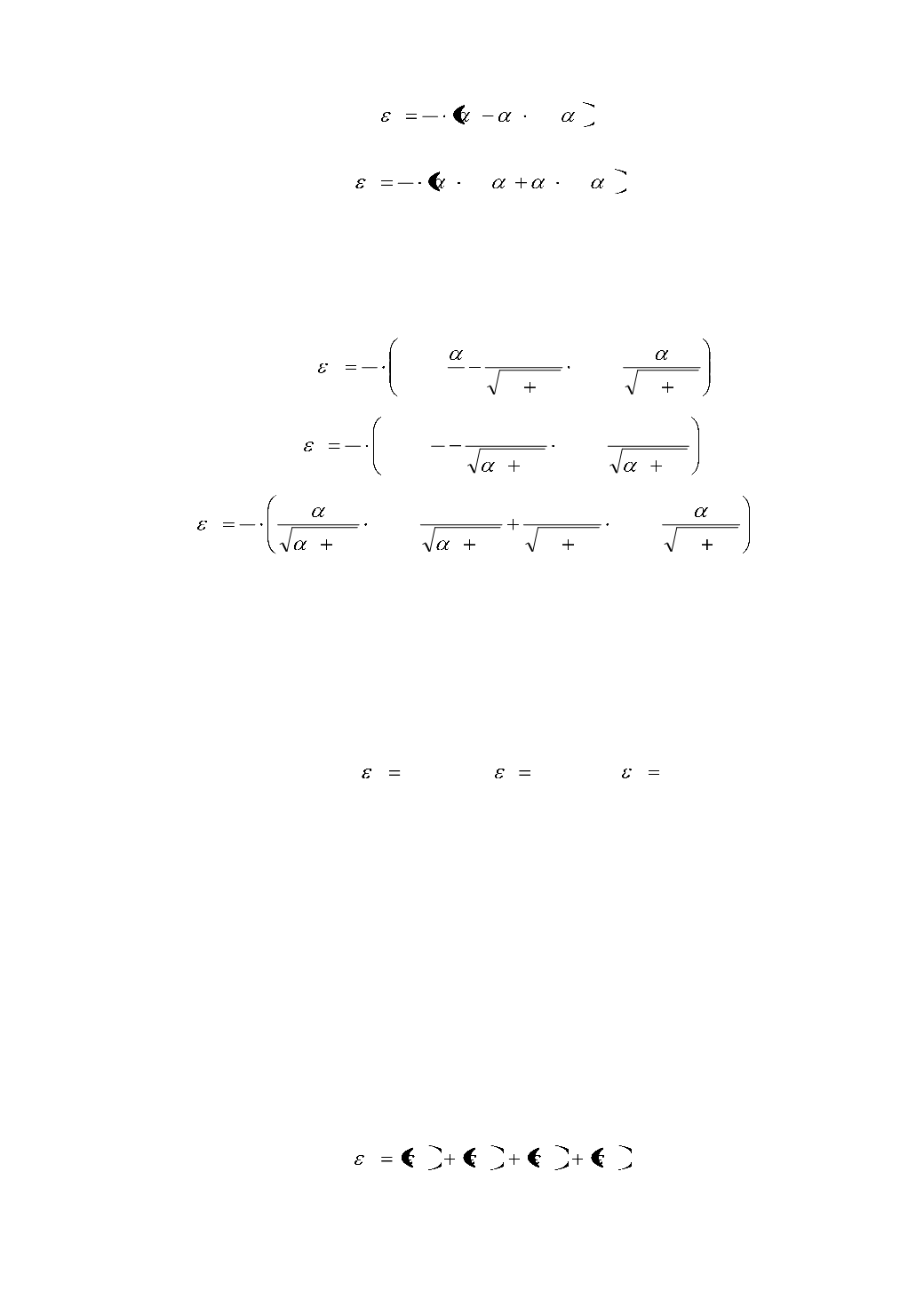
Подставляя в полученные равенства значения углов α
i
, имеем оконча-
тельно:
;
2
2
2
2
2
h b
arctg
h b
h
h
arctg
L
X
(2.9)
;
2
2
2
2
2
h
b
arctg
h
h
h
b
arctg
L
Y
(2.10)
.
h b
arctg
h b
b
h
b
arctg
h
L
Z
2
2
2
2
2
2
2
2
2
(2.11)
Согласно определению вектора излучения для рассмотренного частно-
го случая расположения исследуемой точки, проекции вектора излучения на
координатные оси численно равны значениям облученности координатных
плоскостей в точке
О
:
;
YOZ
X
E
;
XOZ
Y
E
XOY
Z
E
. (2.12)
Эти равенства определяются тем, что при исследуемом расположении
точки
О
координатные плоскости не пересекают прямоугольного излучателя.
В тех случаях, когда проекции исследуемой точки поля на плоскость излуча-
теля не совпадают с одной из вершин, необходимо пользоваться теми же рас-
четными уравнениями, производя расчет по одной из схем, указанных на ри-
сунке 2.3.
Для случая, когда проекция исследуемой точки на плоскость излучате-
ля попадает внутрь его контура (схема 1), проекция вектора излучения на ось
Z определится как [83]
4
3
2
1
Z
Z
Z
Z
Z
, (2.13)
Электронная Научная СельскоХозяйственная Библиотека









