
147
где
2
i
– отражает вариацию за счет всех остальных факторов,
то есть является остаточной дисперсией:
n
ост
i
2
^
2
2
)у- (у
. (5.9)
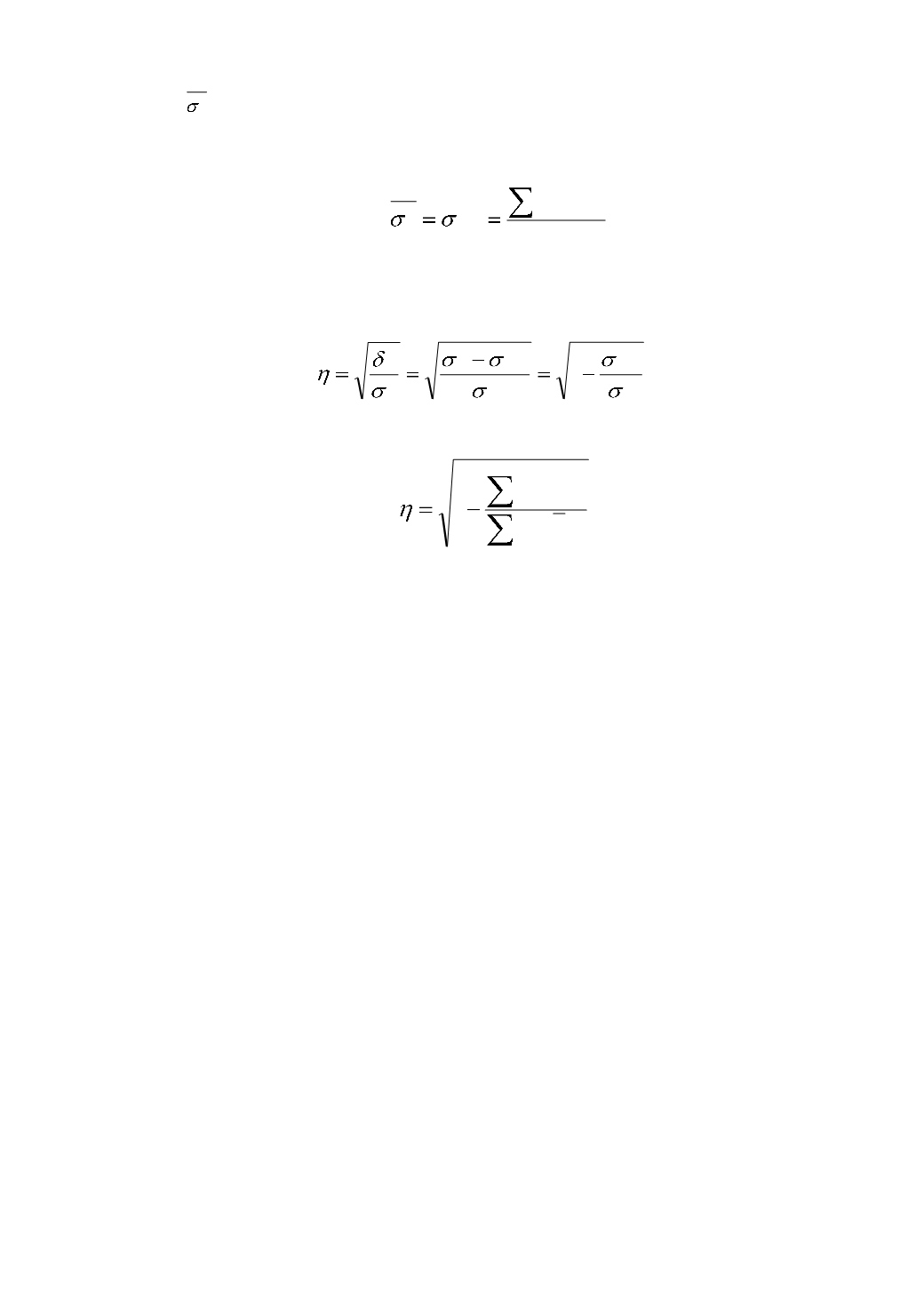
Тогда формула теоретического корреляционного отношения примет
вид:
2
2
2
2
2
2
2
1
ост
ост
, (5.10)
или
2
2
^
)у-(у
)у-(у
1
. (5.11)
Подкоренное выражение корреляционного отношения представляет
собой коэффициент детерминации (меры определенности, причинности).
Коэффициент детерминации показывает долю вариации результатив-
ного признака под влиянием вариации признака-фактора.
При криволинейных связях теоретическое корреляционное отношение,
исчисляемое по формулам (5.10) и (5.11), часто называют индексом корреля-
ции
R
. Как видно из формул, корреляционное отношение может находиться в
пределах от 0 до 1. Чем ближе корреляционное отношение к 1, тем связь
между признаками теснее.
Для шестнадцати опытных и шестнадцати промоделированных кривых
по вышеописанным моделям в среде Программного комплекса «Моделиро-
вание в технических устройствах» определены значения
η
, которые состави-
ли не менее 0,98, при этом
F
расч
>
F
табл
.
Для качественной оценки тесноты связи на основе показателя теорети-
ческого корреляционного отношения воспользуемся соотношениями Чэддока
(таблица 5.1) [77].
Электронная Научная Сельск Хозяйственная Библиотека









