
224
Для второго критерия оптимизации (крошимости гранул) тоже прове-
рена воспроизводимость опытов по критерию Кохрена.
Табличное значение
ТАБЛ
G
=0,373›
РАСЧ
G
=0,169.
Численно коэффициенты уравнения равны:
0
b
=6,0999;
1
b
=2,666;
2
b
=1,25;
12
b
=0,8;
11
b
=0,0607;
22
b
=0,0605.
Доверительные интервалы для них:
0
b
=±0,262;
i
b
=±0,394;
ii
b
=±0,644;
ji
b
=±0,788.
Сравнение доверительных интервалов и численных значений коэффи-
циентов показывает, что значимость коэффициентов при квадратичных чле-
нах уравнения не подтверждается.
Проверка адекватности без этих двух членов одновременно показала,
что уровень значимости снижается до 0,10. С целью сохранения уровня зна-
чимости уравнения для 95% надежности при дальнейшем анализе сохранены
все коэффициенты.
Окончательно уравнение регрессии для крошимости гранул имеет вид:
Z
1
= 6,0999+2,666Х
1
+1,25Х
2
+0,8Х
1
Х
2
+0,0607Х
1
2
+0,0605Х
2
2
. (4.71)
Адекватность его подтверждена тестированием на сходимость расчет-
ных и опытных данных по критерию Фишера,
Ф
ТЕСТ
= 0,993.
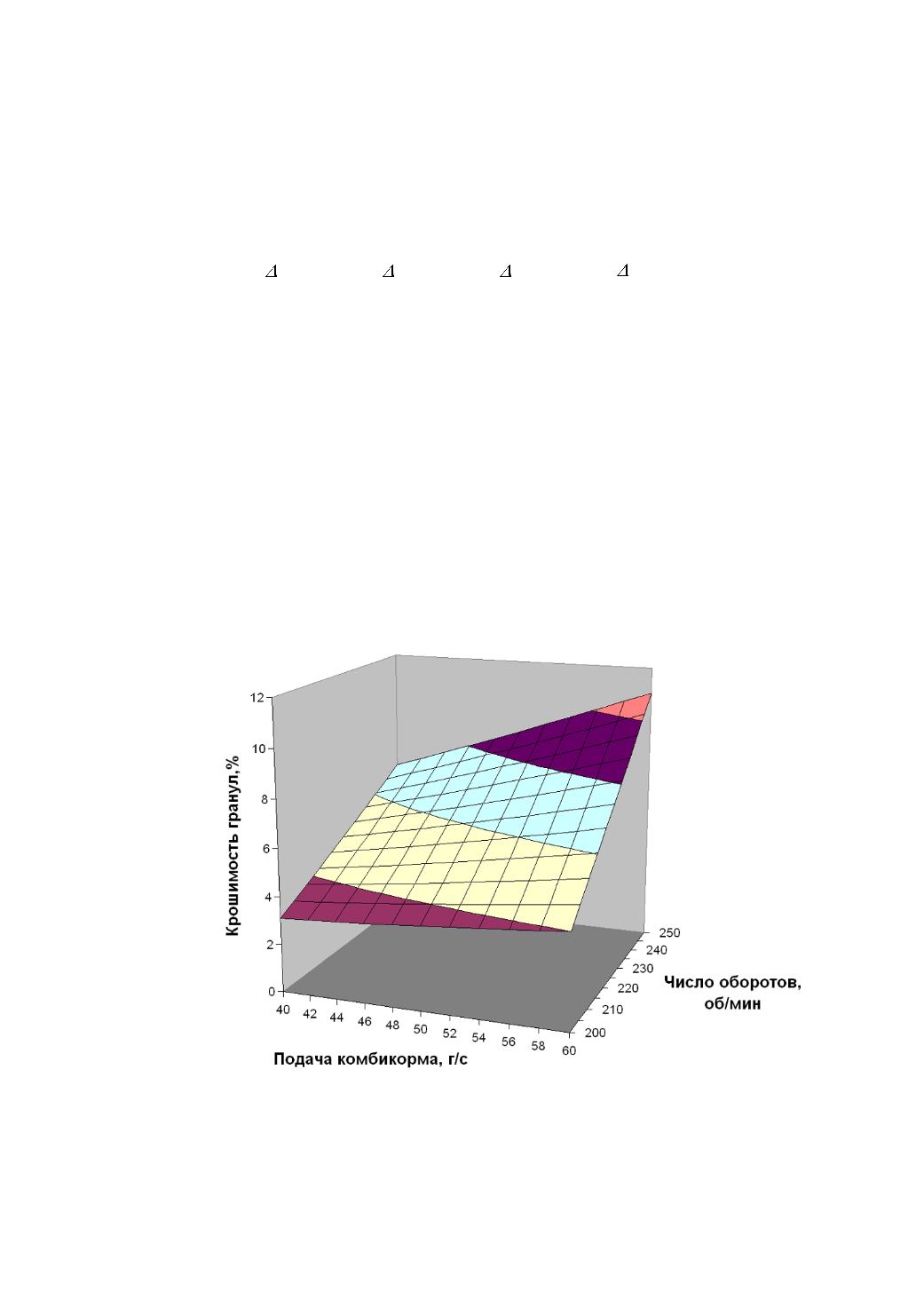
Наглядное представление поверхности отклика приведено на рисунке
4.20.
Рисунок 4.20 – Поверхность отклика функции крошимости гранул
(матрица с круглыми каналами прессования и гладкий валец)
Электронная Научная СельскоХозяйственная Библиотека









